Wat betekent regressie? Een eenvoudige uitleg

20 May 2024
nl
Murphy

Wat is regressie nou eigenlijk? Het klinkt misschien ingewikkeld, maar het is eigenlijk een heel handig statistisch hulpmiddel. Stel je voor dat je wilt weten hoe de prijs van een huis afhangt van de grootte. Regressie helpt je om die relatie te begrijpen.

Regressieanalyse is een methode om de relatie tussen twee of meer variabelen te onderzoeken. Eén variabele is de afhankelijke variabele (bijvoorbeeld de huisprijs) en de andere variabelen zijn de onafhankelijke variabelen (bijvoorbeeld de grootte van het huis). Regressie probeert te voorspellen hoe de afhankelijke variabele verandert als de onafhankelijke variabelen veranderen.

Denk bijvoorbeeld aan de relatie tussen temperatuur en ijsverkoop. Op warme dagen wordt er meer ijs verkocht. Met regressie kun je een model maken dat voorspelt hoeveel ijs er verkocht wordt bij een bepaalde temperatuur. Dit model kan dan gebruikt worden om de ijsverkoop te voorspellen op toekomstige warme dagen.

De term "regressie" komt van de statisticus Sir Francis Galton. Hij ontdekte dat de lengte van kinderen van lange ouders neigde naar het gemiddelde. Dit noemde hij "regressie naar het gemiddelde". Tegenwoordig wordt regressie gebruikt voor veel meer dan alleen het bestuderen van lengte.

Regressie is belangrijk in veel vakgebieden, zoals economie, marketing, en wetenschappelijk onderzoek. Het helpt ons om patronen te ontdekken en voorspellingen te doen. Maar het is belangrijk om te onthouden dat regressie geen perfect hulpmiddel is. Er zijn altijd factoren die niet in het model worden meegenomen.

Een eenvoudig voorbeeld van regressie is het voorspellen van de verkoopprijs van een huis op basis van de woonoppervlakte. We kunnen een lineair regressiemodel gebruiken om een rechte lijn te vinden die de relatie tussen deze twee variabelen beschrijft. De formule voor een eenvoudige lineaire regressie is Y = a + bX, waarbij Y de afhankelijke variabele (verkoopprijs), X de onafhankelijke variabele (woonoppervlakte), a de intercept en b de helling van de lijn is.

Een voordeel van regressie is dat het ons helpt trends te identificeren. Door de relatie tussen variabelen te analyseren, kunnen we patronen en trends identificeren die anders misschien niet duidelijk zouden zijn. Een ander voordeel is dat het ons in staat stelt voorspellingen te doen. Door een regressiemodel te gebruiken, kunnen we schattingen maken van de waarde van de afhankelijke variabele op basis van de waarden van de onafhankelijke variabelen.

Een derde voordeel van regressie is dat het ons kan helpen bij het nemen van beslissingen. Door de impact van verschillende variabelen op een uitkomst te begrijpen, kunnen we weloverwogen beslissingen nemen op basis van data-gedreven inzichten.

Voor- en Nadelen van Regressie

Voordelen	Nadelen
Identificeren van trends	Gevoelig voor outliers
Doen van voorspellingen	Vereist aannames over de data
Helpt bij besluitvorming	Kan complex zijn om te interpreteren

Veelgestelde vragen:

1. Wat is regressie? Regressie is een statistische methode om de relatie tussen variabelen te modelleren.

2. Wat is een regressiemodel? Een regressiemodel is een wiskundige vergelijking die de relatie tussen variabelen beschrijft.

3. Wat is lineaire regressie? Lineaire regressie is een type regressie waarbij de relatie tussen variabelen wordt gemodelleerd als een rechte lijn.

4. Wat is meervoudige regressie? Meervoudige regressie is een type regressie met meerdere onafhankelijke variabelen.

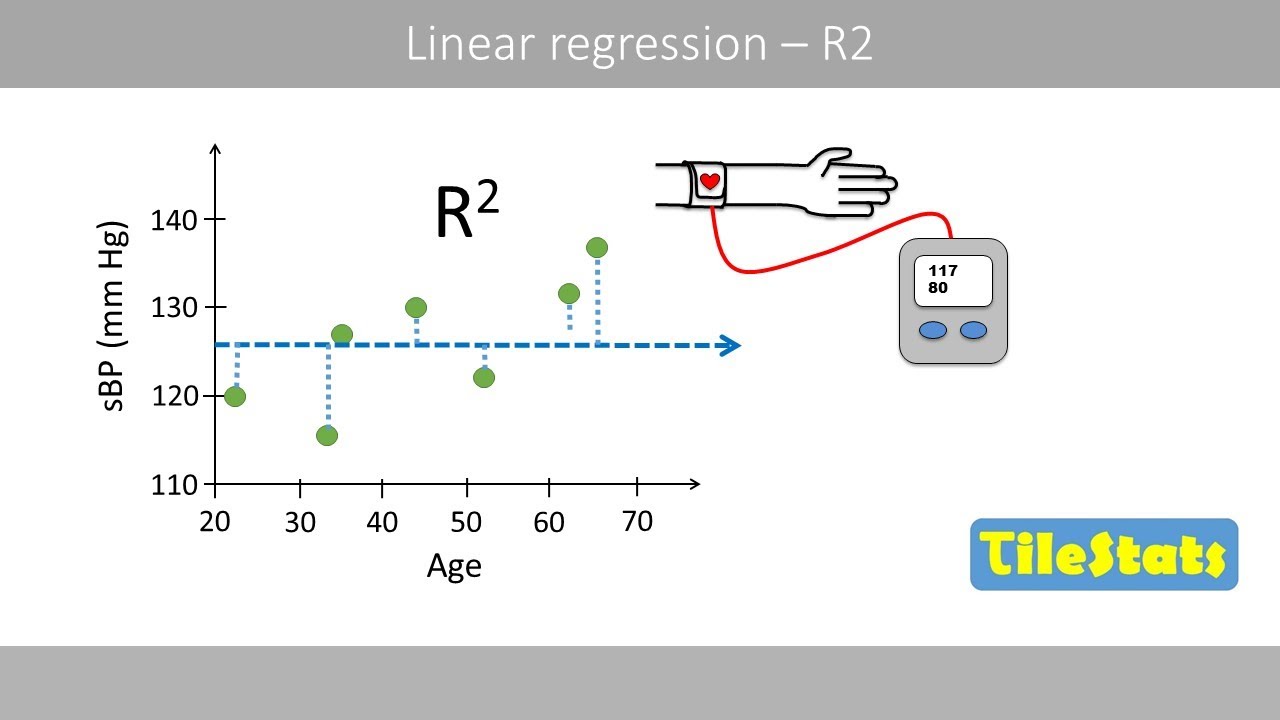
5. Wat is de R-kwadraat waarde? De R-kwadraat waarde geeft aan hoe goed het model de data fit.

6. Wat zijn outliers? Outliers zijn datapunten die ver van de andere datapunten liggen.

7. Hoe interpreteer je een regressiemodel? De interpretatie van een regressiemodel hangt af van de specifieke variabelen en het type regressie.

8. Waar kan ik meer leren over regressie? Er zijn veel online bronnen en boeken beschikbaar over regressieanalyse.

Tips en trucs: Zorg voor schone data, kies het juiste regressiemodel en controleer de aannames van het model.

Kortom, regressie is een krachtig hulpmiddel om relaties tussen variabelen te onderzoeken en voorspellingen te doen. Het is belangrijk om de beperkingen van regressie te begrijpen en de resultaten zorgvuldig te interpreteren. Door regressie te gebruiken, kunnen we waardevolle inzichten verkrijgen uit data en betere beslissingen nemen. De mogelijkheden van regressieanalyse zijn eindeloos en het is een essentieel instrument voor iedereen die met data werkt. Het begrip van regressie opent deuren naar een dieper inzicht in de wereld om ons heen en stelt ons in staat om weloverwogen beslissingen te nemen op basis van data-gedreven inzichten. Verder onderzoek en toepassing van regressieanalyse is essentieel voor vooruitgang in diverse vakgebieden en draagt bij aan een beter begrip van complexe fenomenen.