Ontdek de magie van zeshoeken: hoeken en meer!

26 Jul 2024
nl
Murphy

Heb je je ooit afgevraagd waarom honingraten zo perfect symmetrisch zijn? Of waarom bepaalde tegels altijd naadloos in elkaar lijken te passen? Het antwoord ligt in een fascinerende geometrische vorm: de zeshoek! En het geheim achter zijn veelzijdigheid schuilt in de binnenhoeken.

Laten we eens dieper ingaan op de wondere wereld van zeshoeken en hun binnenhoeken. We ontdekken hoe deze hoeken worden berekend, waarom ze zo belangrijk zijn en waar we ze overal om ons heen tegenkomen. Bereid je voor op een reis vol verrassende weetjes en praktische toepassingen!

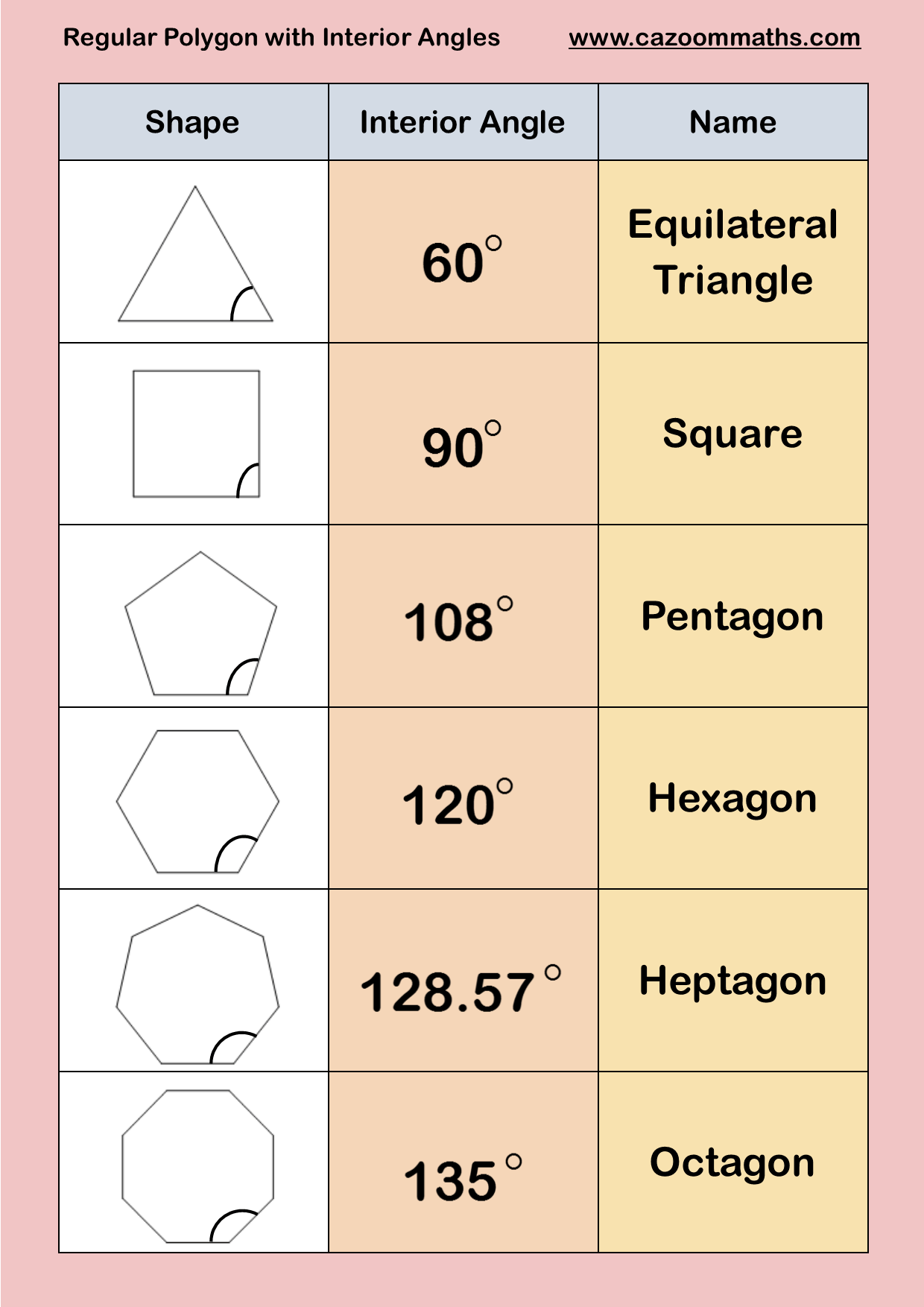
Een zeshoek is een veelhoek met zes zijden en zes hoeken. Maar wat deze vorm zo bijzonder maakt, is de unieke eigenschap van zijn binnenhoeken. Elke binnenhoek van een regelmatige zeshoek meet precies 120 graden. Deze eigenschap heeft geleid tot talloze fascinerende toepassingen in de natuur, architectuur, kunst en technologie.

Al sinds de oudheid zijn mensen gefascineerd door zeshoeken. Denk maar aan de honingraten van bijen, een waar wonder van efficiëntie en stevigheid. Of de spectaculaire basaltkolommen van de Giant's Causeway, gevormd door vulkanische activiteit. Zelfs in de moleculaire structuur van grafeen, een revolutionair materiaal, vinden we de kenmerkende zeshoekige vorm terug.

De populariteit van de zeshoek is geen toeval. Naast zijn esthetische aantrekkingskracht, biedt deze vorm tal van voordelen. Zo zorgt de hoek van 120 graden voor een optimale verdeling van krachten, waardoor structuren zeer stabiel en duurzaam zijn. Bovendien kunnen zeshoeken naadloos aan elkaar worden gekoppeld, zonder verspilling van ruimte. Dit maakt ze ideaal voor tegels, patronen en zelfs de opslag van data.

Of je nu een wiskundewizard bent of gewoon nieuwsgierig naar de wereld om je heen, zeshoeken en hun binnenhoeken bieden een fascinerend inkijkje in de schoonheid en efficiëntie van geometrische vormen. Dus de volgende keer dat je een honingraat ziet, een tegelvloer bewondert of een bijenkorf van dichtbij bekijkt, neem dan even de tijd om de kracht van de zeshoek te waarderen!

Voor- en nadelen van zeshoekige structuren

Hoewel zeshoeken tal van voordelen bieden, zijn er ook enkele nadelen om rekening mee te houden.

Voordelen	Nadelen
Efficiënt ruimtegebruik	Complexere constructie dan vierkanten
Hoge stabiliteit en sterkte	Niet altijd compatibel met bestaande rechthoekige structuren
Esthetisch aantrekkelijk	Beperkte ontwerpmogelijkheden in vergelijking met onregelmatige vormen

Veelgestelde vragen over binnenhoeken van zeshoeken

Hier zijn enkele veelgestelde vragen met antwoorden over binnenhoeken van zeshoeken:

1. Wat is de som van de binnenhoeken van een zeshoek?

De som van de binnenhoeken van een zeshoek is altijd 720 graden.

2. Hoe bereken ik de grootte van één binnenhoek van een regelmatige zeshoek?

Deel de totale som van de binnenhoeken (720 graden) door het aantal hoeken (6) om de grootte van één binnenhoek te vinden: 720 graden / 6 = 120 graden.

3. Zijn alle zeshoeken regelmatig?

Nee, niet alle zeshoeken zijn regelmatig. Een regelmatige zeshoek heeft zes gelijke zijden en zes gelijke hoeken. Een onregelmatige zeshoek kan zijden en hoeken van verschillende grootte hebben.

4. Waar kan ik meer informatie vinden over zeshoeken en hun eigenschappen?

Je kunt meer informatie vinden over zeshoeken op websites zoals Wikipedia, wiskundige naslagwerken en online leerplatforms zoals Khan Academy.

De zeshoek, met zijn unieke eigenschap van 120 graden binnenhoeken, is een bewijs van de elegantie en efficiëntie die we in de geometrie terugvinden. Van de natuur tot aan onze technologie, de zeshoekige vorm blijft ons verbazen en inspireren. Hopelijk heeft dit artikel je een nieuwe waardering gegeven voor deze fascinerende vorm en zijn ontelbare toepassingen.