Stel je voor: een honingraat, perfect gevormd met identieke zeshoekige cellen. Of denk aan de structuur van een sneeuwvlok, een symfonie van zeshoekige vormen. Wat maakt deze zeshoeken zo bijzonder? Een deel van hun aantrekkingskracht ligt in hun unieke geometrie, met name in de buitenhoeken.
Een buitenhoek van een veelhoek ontstaat door één zijde te verlengen en de hoek te meten tussen deze verlengde zijde en de aangrenzende zijde. In een regelmatige zeshoek, met zijn zes gelijke zijden en zes gelijke hoeken, heeft elke buitenhoek een fascinerende eigenschap: ze zijn allemaal precies 60 graden!
Deze consistente hoekgrootte heeft belangrijke gevolgen. Het is de reden waarom honingraten zo efficiënt ruimte kunnen vullen zonder verspilling. Het verklaart ook de prachtige symmetrie die we in sneeuwvlokken en andere natuurlijke formaties zien.
De geschiedenis van zeshoeken gaat terug tot de oudheid. Oude beschavingen waren al gefascineerd door hun unieke eigenschappen. De Griekse wetenschapper Pythagoras bestudeerde zeshoeken al in de 6e eeuw voor Christus. Hij ontdekte dat zes gelijkzijdige driehoeken samen een perfecte zeshoek vormen.
Vandaag de dag komen we zeshoeken tegen in diverse toepassingen. Vanwege hun sterkte en stabiliteit worden ze gebruikt in de architectuur, bijvoorbeeld in bruggen en gebouwen. In de natuur vinden we ze terug in honingraten, insectenogen en zelfs de structuur van bepaalde moleculen.
Voor- en Nadelen van Buitenhoeken in Regelmatige Zeshoeken
Hoewel we niet echt kunnen spreken van voor- en nadelen van een geometrisch concept, kunnen we wel kijken naar de voordelen en interessante aspecten van de buitenhoeken in regelmatige zeshoeken:
| Voordeel | Uitleg |
|---|---|
| Efficiënte ruimtevulling | Zeshoeken kunnen naadloos aan elkaar worden gelegd zonder dat er ruimte verloren gaat. Dit komt doordat de buitenhoeken van 60 graden perfect optellen tot 360 graden. |
| Sterke structuur | De gelijke hoeken en zijden van een zeshoek zorgen voor een gelijkmatige verdeling van krachten, waardoor structuren stabieler zijn. |
| Esthetische aantrekkingskracht | De symmetrie en regelmaat van zeshoeken worden vaak als esthetisch aantrekkelijk ervaren. |
Veelgestelde Vragen over Buitenhoeken in Regelmatige Zeshoeken
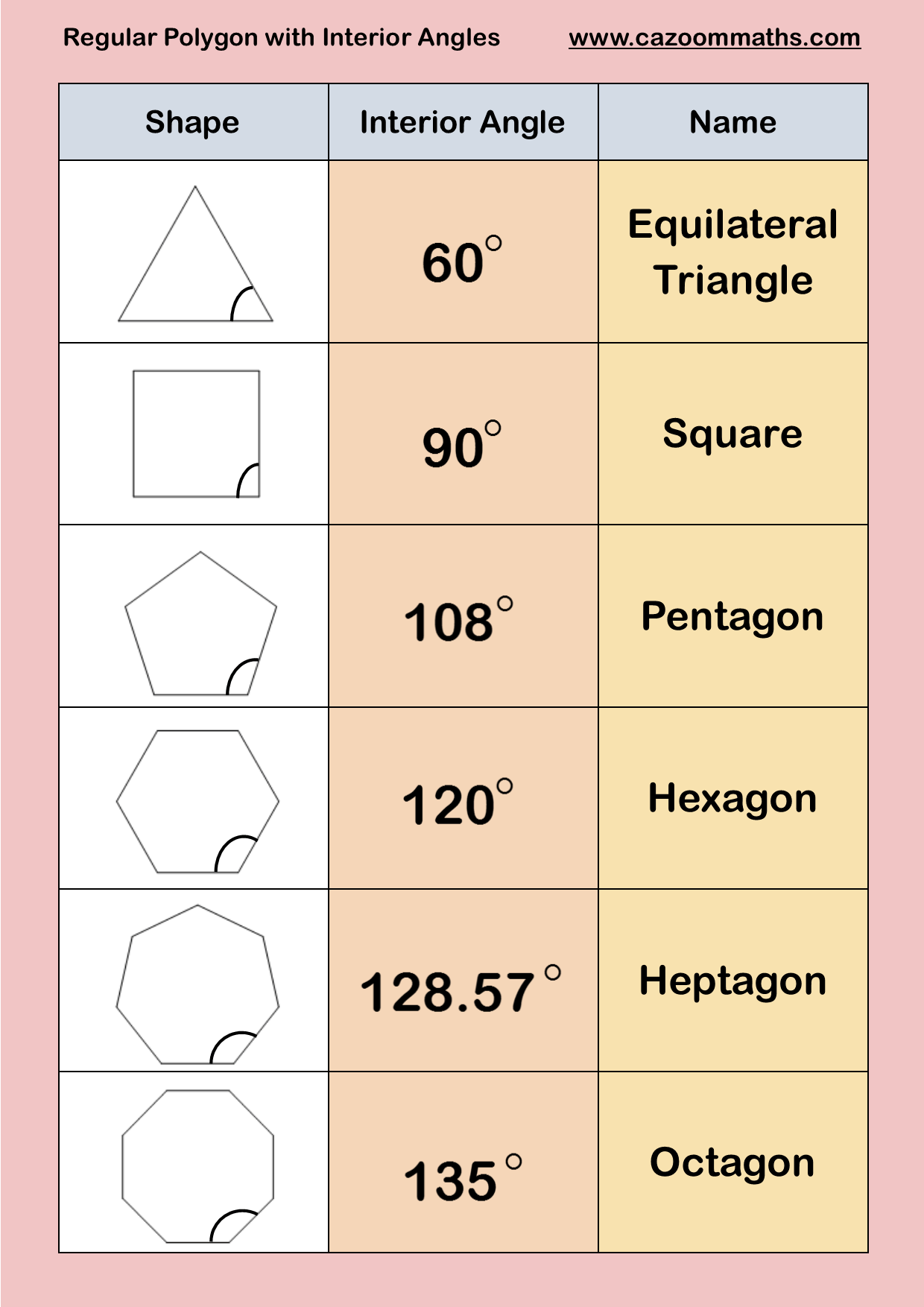
1. Hoe bereken je de grootte van een buitenhoek in een regelmatige zeshoek?
De som van alle buitenhoeken van elke veelhoek is altijd 360 graden. Omdat een regelmatige zeshoek zes gelijke buitenhoeken heeft, is elke buitenhoek 360 graden / 6 = 60 graden.
2. Wat is de relatie tussen binnen- en buitenhoeken in een zeshoek?
Een binnenhoek en de bijbehorende buitenhoek vormen altijd samen een gestrekte hoek van 180 graden. In een regelmatige zeshoek is elke binnenhoek 120 graden (180 graden - 60 graden).
3. Waarom zijn zeshoeken zo sterk?
De gelijke hoeken en zijden van een zeshoek zorgen voor een gelijkmatige verdeling van krachten, waardoor structuren stabieler zijn. Denk aan de structuur van honingraten: ze kunnen veel gewicht dragen ten opzichte van hun lichte gewicht.
4. Waar kan ik meer leren over zeshoeken en hun eigenschappen?
Er zijn talloze bronnen beschikbaar! Zoek online naar "geometrie van zeshoeken" of bekijk wiskundeboeken over veelhoeken.
5. Wat zijn enkele voorbeelden van zeshoeken in de natuur?
Honingraten, sneeuwvlokken, de ogen van insecten en de kristalstructuur van sommige mineralen vertonen allemaal zeshoekige patronen.
6. Hoe worden zeshoeken gebruikt in de architectuur?
Vanwege hun sterkte en efficiënte ruimtebenutting worden zeshoeken gebruikt in bruggen, gebouwen, bestrating en andere constructies.
7. Wat is de betekenis van zeshoeken in kunst en design?
Zeshoeken worden vaak gebruikt in kunst en design vanwege hun esthetische aantrekkingskracht. Ze creëren een gevoel van harmonie, balans en orde.
8. Kan ik zelf zeshoekige patronen maken?
Absoluut! Met een beetje oefening kun je zeshoeken tekenen, vouwen of zelfs bouwen met behulp van eenvoudige materialen.
Conclusie
De buitenhoek van een regelmatige zeshoek, met zijn constante waarde van 60 graden, is een sleutel tot vele fascinerende eigenschappen. Het verklaart de efficiënte ruimtevulling, de structurele stabiliteit en de esthetische aantrekkingskracht van zeshoekige patronen. Van de honingraten in de natuur tot de bouwwerken van de mens, de zeshoek bewijst dat geometrie niet alleen een abstract concept is, maar een krachtig hulpmiddel in ons begrip van de wereld om ons heen. Dus de volgende keer dat je een zeshoek tegenkomt, neem dan even de tijd om de schoonheid en elegantie van zijn buitenhoeken te waarderen!
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
How To Calculate Sum Of Interior Angles - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq
How To Find Interior Angles Of Polygons - The Brass Coq
Work Out The Sum Of Interior Angles - The Brass Coq
exterior angle of a regular hexagon - The Brass Coq