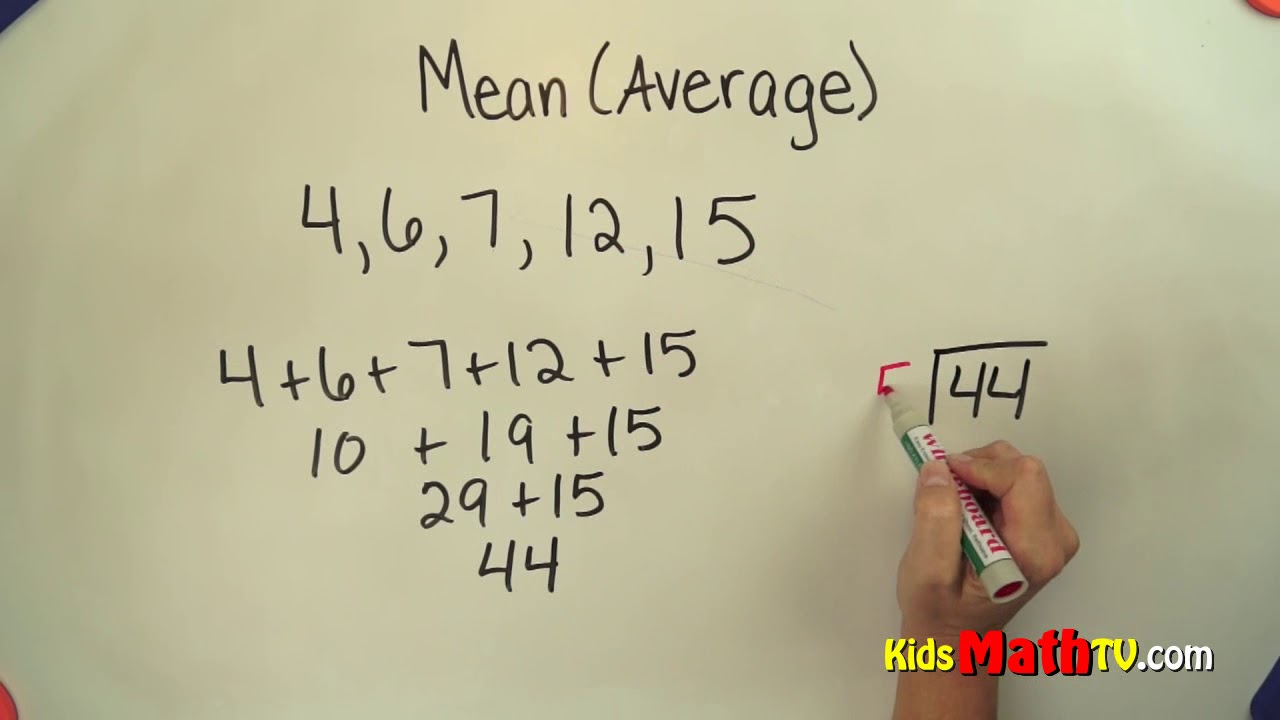Het Gemiddelde: Een Kernbegrip in de Wiskunde

04 Jul 2024
nl
Murphy

Stel je voor: je hebt een handvol knikkers, allemaal met verschillende groottes. Hoe vind je de "typische" grootte van een knikker? Dit is waar het gemiddelde in de wiskunde om de hoek komt kijken. Het gemiddelde, ook wel het rekenkundig gemiddelde genoemd, is een centraal begrip in de statistiek en wiskunde, dat ons helpt om een representatieve waarde te vinden voor een groep getallen.

Het berekenen van het gemiddelde is een essentiële vaardigheid, niet alleen voor wiskundigen en statistici, maar ook voor iedereen die met data werkt. Van het bepalen van de gemiddelde temperatuur tot het analyseren van verkoopcijfers, het gemiddelde geeft ons waardevolle inzichten in datasets.

Wat is nu precies het gemiddelde in wiskundige termen? Simpel gezegd, het gemiddelde is de som van alle getallen in een dataset, gedeeld door het totaal aantal getallen. Het geeft ons een idee van het "midden" van de data.

Het gemiddelde is al eeuwenlang een belangrijk instrument in de wiskunde. Historisch gezien werd het gebruikt door astronomen om de positie van hemellichamen te berekenen en door handelaren om hun winst te bepalen. Vandaag de dag is het gemiddelde onmisbaar in diverse disciplines, van economie tot geneeskunde.

Een van de belangrijkste problemen met het gemiddelde is dat het gevoelig is voor uitschieters. Een extreem hoge of lage waarde in de dataset kan het gemiddelde significant beïnvloeden, waardoor het minder representatief wordt voor de meeste data. Daarom is het belangrijk om naast het gemiddelde ook andere statistische maten, zoals de mediaan en de modus, te bekijken.

De formule voor het gemiddelde is: Gemiddelde = (Som van alle getallen) / (Totaal aantal getallen). Stel, je hebt de volgende cijfers: 7, 8, 9, 10. Het gemiddelde is (7+8+9+10)/4 = 8,5.

Voordelen van het gebruik van het gemiddelde zijn: 1) Eenvoudig te berekenen. 2) Gemakkelijk te begrijpen. 3) Nuttig voor het vergelijken van verschillende datasets.

Stel je wilt je gemiddelde cijfer berekenen. Tel alle cijfers op en deel door het aantal cijfers. Dit geeft je je gemiddelde cijfer.

Checklist voor het berekenen van het gemiddelde: 1) Verzamel alle getallen. 2) Tel de getallen op. 3) Deel de som door het aantal getallen.

Stap-voor-stap handleiding: 1) Schrijf alle getallen op. 2) Gebruik een rekenmachine of tel de getallen handmatig op. 3) Deel de som door het aantal getallen om het gemiddelde te vinden.

Een aanbevolen website voor het leren over statistiek is Khan Academy.

Voor- en Nadelen van het Gemiddelde

Voordelen	Nadelen
Eenvoudig te berekenen	Gevoelig voor uitschieters
Gemakkelijk te begrijpen	Niet altijd representatief voor de gehele dataset

Beste Praktijken: 1) Controleer op uitschieters. 2) Gebruik het gemiddelde in combinatie met andere statistische maten. 3) Zorg ervoor dat de data representatief is. 4) Interpreteer het gemiddelde in de context van de data. 5) Gebruik de juiste eenheden.

Voorbeelden: 1) Gemiddelde leeftijd van studenten. 2) Gemiddelde temperatuur. 3) Gemiddeld inkomen. 4) Gemiddelde score op een toets. 5) Gemiddelde lengte.

Uitdagingen: 1) Uitschieters. Oplossing: Gebruik de mediaan. 2) Scheve data. Oplossing: Gebruik de modus. 3) Kleine datasets. Oplossing: Verzamel meer data.

FAQ: 1) Wat is het gemiddelde? 2) Hoe bereken je het gemiddelde? 3) Wat is het verschil tussen gemiddelde, mediaan en modus? 4) Wanneer is het gemiddelde een goede maat voor centraliteit? 5) Hoe beïnvloeden uitschieters het gemiddelde? 6) Wat zijn andere maten van centraliteit? 7) Waar kan ik meer leren over het gemiddelde?

Tips: Gebruik een rekenmachine. Controleer je berekeningen.

Het gemiddelde is een krachtig instrument om inzicht te krijgen in data. Het is eenvoudig te berekenen en te begrijpen, waardoor het een waardevolle maat is voor centraliteit. Echter, het is belangrijk om bewust te zijn van de beperkingen van het gemiddelde, zoals de gevoeligheid voor uitschieters. Door het gemiddelde te combineren met andere statistische maten en de data zorgvuldig te interpreteren, kunnen we waardevolle conclusies trekken en weloverwogen beslissingen nemen. Het begrijpen van het gemiddelde en hoe het te gebruiken is essentieel voor iedereen die met data werkt, van studenten tot professionals. Het is een fundamenteel concept dat ons helpt om de wereld om ons heen beter te begrijpen.