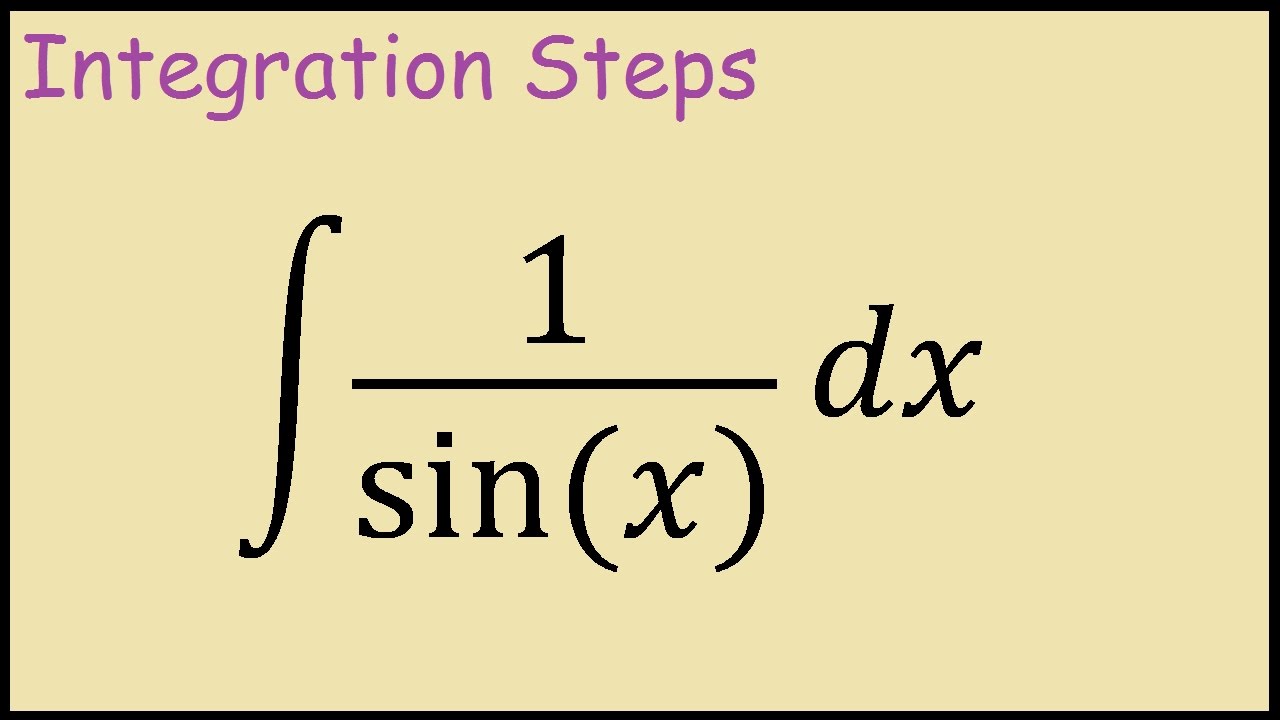Integralen: voor velen roept het woord misschien stoffige schoolboeken en gecompliceerde formules op. Maar achter deze abstracte wiskunde schuilt een krachtig instrument dat ons in staat stelt om complexe problemen te ontrafelen en de wereld om ons heen beter te begrijpen.
Stel je voor dat je de oppervlakte wilt berekenen van een onregelmatig gevormd object. Met traditionele meetkunde zou dit een onmogelijke opgave lijken. Maar met behulp van integralen kunnen we deze uitdaging aan. Door de vorm op te delen in oneindig kleine stukjes, die we vervolgens bij elkaar optellen, kunnen we een accurate benadering van de totale oppervlakte verkrijgen.
Dit principe van integreren, het optellen van oneindig kleine deeltjes, heeft toepassingen in talloze domeinen. Van het berekenen van de baan van een satelliet tot het voorspellen van de verspreiding van een virus, integralen spelen een cruciale rol in ons begrip van de wereld.
Een interessante integraal om te bestuderen is de integraal van sin^(-1)(x^2). Deze integraal combineert trigonometrische functies met machtsfuncties, wat leidt tot een boeiende uitdaging voor wiskundigen. Door gebruik te maken van integratietechnieken zoals substitutie en partiële integratie, kunnen we deze integraal oplossen en de onderliggende schoonheid van de wiskunde ontdekken.
Het begrijpen van integralen is niet alleen essentieel voor wiskundigen en wetenschappers, maar ook voor iedereen die geïnteresseerd is in de werking van de wereld om ons heen. Van de kleinste atomen tot de grootste sterrenstelsels, integralen helpen ons de complexiteit van het universum te doorgronden.
Voor- en nadelen van integreren
Hoewel integreren een krachtig instrument is, is het belangrijk om de voor- en nadelen ervan te erkennen:
| Voordelen | Nadelen |
|---|---|
| Los complexe problemen op | Kan computationeel intensief zijn |
| Brede toepasbaarheid in verschillende domeinen | Vereist een goed begrip van wiskundige concepten |
| Vergroot analytisch denkvermogen | Niet altijd een exacte oplossing mogelijk |
Tips en trucs voor integreren
Integreren kan een uitdaging lijken, maar met de juiste aanpak kan het een lonende ervaring zijn. Hier zijn enkele tips om je te helpen:
- Oefen regelmatig met verschillende soorten integralen.
- Maak gebruik van online hulpmiddelen en software om je vaardigheden te verbeteren.
- Werk samen met anderen en leer van hun aanpak.
- Wees niet bang om fouten te maken, het is een essentieel onderdeel van het leerproces.
- Geniet van de schoonheid en de kracht van integreren!
Conclusie
Integralen vormen een fascinerend en essentieel onderdeel van de wiskunde, met toepassingen in talloze domeinen. Van het berekenen van oppervlakten tot het modelleren van complexe systemen, integralen stellen ons in staat om de wereld om ons heen beter te begrijpen. Hoewel het beheersen van integratietechnieken oefening en towijding vereist, is de beloning groot. Door de kracht van integreren te ontsluiten, openen we de deur naar een wereld van mogelijkheden en verdiepen we ons begrip van het universum.
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq
integrate sin -1 x 2 - The Brass Coq