De Verborgen Symmetrie: Ontdek de Wereld van Cos ix Cosh x Proof

16 Aug 2024
nl
Murphy

De wereld van de wiskunde zit vol met verborgen verbindingen en elegante symmetrieën. Een van die fascinerende relaties is de identiteit cos ix = cosh x, een formule die de trigonometrische functie cosinus verbindt met de hyperbolische cosinusfunctie via het imaginaire getal i. Deze ogenschijnlijk eenvoudige vergelijking opent de deur naar een rijk wiskundig landschap, vol intrigerende concepten en praktische toepassingen.

De identiteit cos ix = cosh x is niet zomaar een abstracte formule; het is een brug die twee schijnbaar verschillende wiskundige gebieden met elkaar verbindt: trigonometrie, die zich bezighoudt met hoeken en zijden van driehoeken, en hyperbolische functies, die hun wortels hebben in de geometrie van hyperbolen.

De oorsprong van deze identiteit kan worden herleid tot de 18e eeuw, tijdens de ontwikkeling van de complexe analyse. Wiskundigen zoals Leonhard Euler begonnen de eigenschappen van complexe getallen te onderzoeken en ontdekten daarbij de diepe band tussen exponentiële functies, trigonometrische functies en hyperbolische functies.

De identiteit cos ix = cosh x is niet alleen een bewijs van de elegantie van de wiskunde, maar heeft ook praktische toepassingen in verschillende wetenschappelijke en technische disciplines. In de natuurkunde wordt het bijvoorbeeld gebruikt bij de beschrijving van golven, trillingen en elektromagnetische velden. In de elektrotechniek speelt het een rol in de analyse van wisselstroomcircuits.

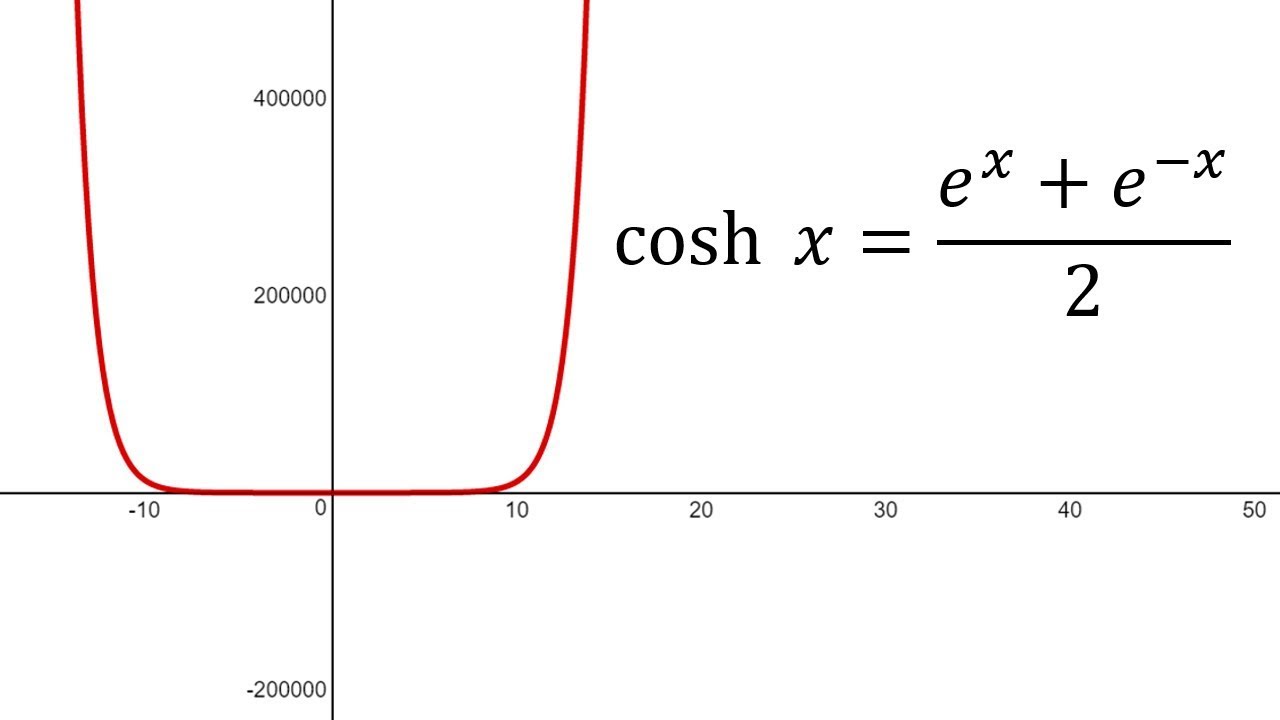
Om de identiteit cos ix = cosh x volledig te begrijpen, moeten we eerst de basisprincipes van complexe getallen en hyperbolische functies begrijpen. Een complex getal wordt gedefinieerd als een getal van de vorm a + bi, waarbij a en b reële getallen zijn en i de imaginaire eenheid is, gedefinieerd als de vierkantswortel van -1. Hyperbolische functies, zoals de hyperbolische cosinus (cosh), worden gedefinieerd met behulp van exponentiële functies. De hyperbolische cosinus van x wordt gedefinieerd als (e^x + e^-x)/2.

De identiteit cos ix = cosh x kan worden bewezen met behulp van de machtreeksrepresentaties van de cosinus- en hyperbolische cosinusfuncties. Door ix te substitueren in de machtreeks voor cosinus en de machtreeks voor hyperbolische cosinus te gebruiken, zien we dat de twee reeksen identiek zijn, wat de identiteit bewijst.

De identiteit cos ix = cosh x heeft vele voordelen in de wiskunde en de wetenschap. Ten eerste biedt het een manier om trigonometrische functies te definiëren en te manipuleren in het complexe vlak, wat nieuwe mogelijkheden opent voor wiskundige analyse. Ten tweede vereenvoudigt het de oplossing van bepaalde differentiaalvergelijkingen die voorkomen in de natuurkunde en de techniek. Ten derde biedt het een beter begrip van de relatie tussen trigonometrische functies en hyperbolische functies, die nuttig zijn in verschillende toepassingen.

De identiteit cos ix = cosh x is een krachtig hulpmiddel voor het oplossen van problemen in de wiskunde, natuurkunde en techniek. Door de relatie tussen trigonometrische functies en hyperbolische functies te gebruiken, kunnen we complexe problemen vereenvoudigen en elegante oplossingen vinden.

De identiteit cos ix = cosh x is een prachtig voorbeeld van de schoonheid en kracht van de wiskunde. Het herinnert ons eraan dat er diepe en onverwachte verbanden bestaan tussen schijnbaar verschillende concepten, en het inspireert ons om te blijven zoeken naar nieuwe kennis en begrip in de wereld om ons heen.