Stel je een wereld voor zonder vergelijkingen. Hoe zouden we dan bepalen of we genoeg geld hebben voor die ene aankoop, of dat de temperatuur hoog genoeg is om in korte broek naar buiten te gaan? Het groter of gelijk aan teken (≥) speelt hierin een cruciale rol, en vormt de basis voor talloze beslissingen en berekeningen in ons dagelijks leven, van alledaagse situaties tot complexe wetenschappelijke formules.
Dit onopvallende symbool, bestaande uit een horizontale streep met een verticale streep eronder, heeft een rijke geschiedenis en een verrassend brede toepassing. Het stelt ons in staat om waarden te vergelijken en te bepalen of een getal groter is dan of gelijk is aan een ander getal. Deze ogenschijnlijk simpele functie heeft enorme implicaties voor diverse disciplines, waaronder wiskunde, natuurkunde, informatica en economie.
In deze gids duiken we diep in de wereld van het groter of gelijk aan teken. We verkennen de oorsprong, de betekenis en de praktische toepassingen van dit essentiële wiskundige symbool. Van eenvoudige voorbeelden tot complexere scenario's, we zullen de kracht en veelzijdigheid van ≥ ontrafelen.
Het 'groter dan of gelijk aan' teken is fundamenteel in de wiskunde. Het wordt gebruikt in ongelijkheden, die op hun beurt weer essentieel zijn voor het oplossen van problemen in algebra, calculus en andere wiskundige disciplines. Het begrip van dit teken is cruciaal voor het oplossen van vergelijkingen en het visualiseren van wiskundige relaties.
Het symbool ≥ is essentieel voor het definiëren van intervallen en domeinen van functies. Denk bijvoorbeeld aan de voorwaarde x ≥ 0, die aangeeft dat x alle niet-negatieve getallen kan vertegenwoordigen. Dit concept is fundamenteel voor het begrijpen en toepassen van wiskundige concepten in de praktijk.
Het groter of gelijk aan teken vindt zijn oorsprong in de ontwikkeling van de wiskundige notatie. Hoewel de precieze oorsprong moeilijk te achterhalen is, is het waarschijnlijk dat het symbool geleidelijk is ontstaan uit de behoefte om vergelijkingen efficiënter en duidelijker weer te geven.
Een simpel voorbeeld: "De temperatuur moet minstens 18 graden zijn om buiten te zwemmen." Dit kan wiskundig worden weergegeven als T ≥ 18, waarbij T staat voor de temperatuur.
Voordelen van het gebruik van het groter of gelijk aan teken:
1. Duidelijkheid: Het symbool ≥ biedt een beknopte en universeel begrepen manier om de relatie tussen twee waarden uit te drukken.
2. Efficiëntie: Het gebruik van symbolen zoals ≥ maakt wiskundige uitdrukkingen korter en gemakkelijker te lezen.
3. Precisie: Het teken ≥ laat geen ruimte voor interpretatie, in tegenstelling tot verbale omschrijvingen.
Veelgestelde vragen:
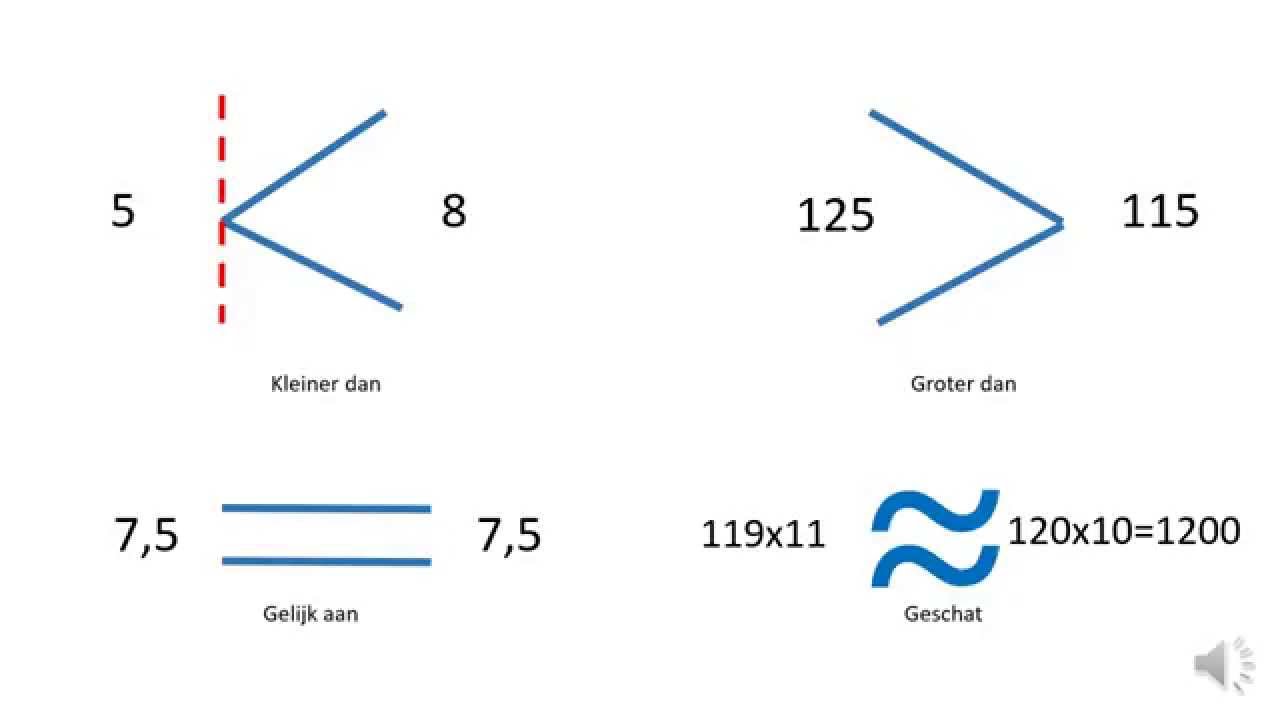
1. Wat is het verschil tussen > en ≥? > betekent 'groter dan', terwijl ≥ 'groter dan of gelijk aan' betekent.
2. Hoe typ ik het ≥ teken op mijn toetsenbord? Dit kan variëren afhankelijk van het besturingssysteem. Vaak is het een combinatie van Alt en een cijfercode.
3. Wordt het ≥ teken ook in programmeren gebruikt? Ja, het wordt gebruikt in conditionele statements en loops.
4. Kan ik ≥ gebruiken met negatieve getallen? Ja, het teken werkt met alle reële getallen.
5. Wat is het tegenovergestelde van ≥? ≤ (kleiner dan of gelijk aan).
6. Hoe gebruik ik ≥ in Excel? Je kunt het direct typen of de functie "ALS" gebruiken met de vergelijking.
7. Wat is het belang van ≥ in statistiek? Het speelt een rol bij het definiëren van kritieke waarden en betrouwbaarheidsintervallen.
8. Waar kan ik meer informatie vinden over wiskundige symbolen? Zoek online naar "wiskundige symbolen" of raadpleeg een wiskundeboek.
Tips en Trucs:
Oefen met het gebruik van het ≥ teken in verschillende contexten om er vertrouwd mee te raken. Experimenteer met verschillende wiskundige problemen en programmeeropdrachten om de veelzijdigheid van het symbool te ontdekken.
Het groter of gelijk aan teken (≥), hoe klein het ook lijkt, is een onmisbaar instrument in de wiskunde, wetenschap en technologie. Het stelt ons in staat om relaties tussen getallen te definiëren, complexe berekeningen uit te voeren en de wereld om ons heen beter te begrijpen. Door de kracht van dit symbool te beheersen, openen we de deur naar een dieper begrip van wiskundige concepten en hun toepassingen in ons dagelijks leven. Van het bepalen van de minimumleeftijd voor een attractie tot het modelleren van complexe systemen, het groter of gelijk aan teken speelt een onmisbare rol. Verken de mogelijkheden en ontdek hoe dit eenvoudige symbool bijdraagt aan de complexiteit en precisie van onze wereld.
Groter dan kleiner dan - The Brass Coq
Groter Dan En Kleiner Dan Tekens De Betekenis En Toepassingen - The Brass Coq
Groter dan kleiner dan en is niet gelijk aan - The Brass Coq
De Watermeloenen Op Het Beeld Tellen En Een Teken Plaatsen Dat Groter - The Brass Coq
Hoe maak je groter dan kleiner dan en gelijk aan teken op het - The Brass Coq
Gelijk aan of groter dan teken - The Brass Coq
Het Kleiner Dan Gelijk Aan Teken Alles Wat Je Moet Weten - The Brass Coq
De Grappige Konijnen Op De Foto Tellen En Een Teken Plaatsen Dat Groter - The Brass Coq
Groter dan of gelijk aan wiskundig symbool Iconen - The Brass Coq
Groter dan of gelijk aan wiskundig symbool Iconen - The Brass Coq
Het Kleiner Dan Gelijk Aan Teken Alles Wat Je Moet Weten - The Brass Coq
Alligator wiskunde Kleiner dan groter dan en gelijk symbool in de - The Brass Coq
Kleiner dan teken Groter dan teken Computerpictogrammen Is gelijk aan - The Brass Coq
De Bloemen Op De Foto Tellen En Een Teken Plaatsen Dat Groter is Dan of - The Brass Coq
Teken Groter Of Gelijk Aan New update - The Brass Coq