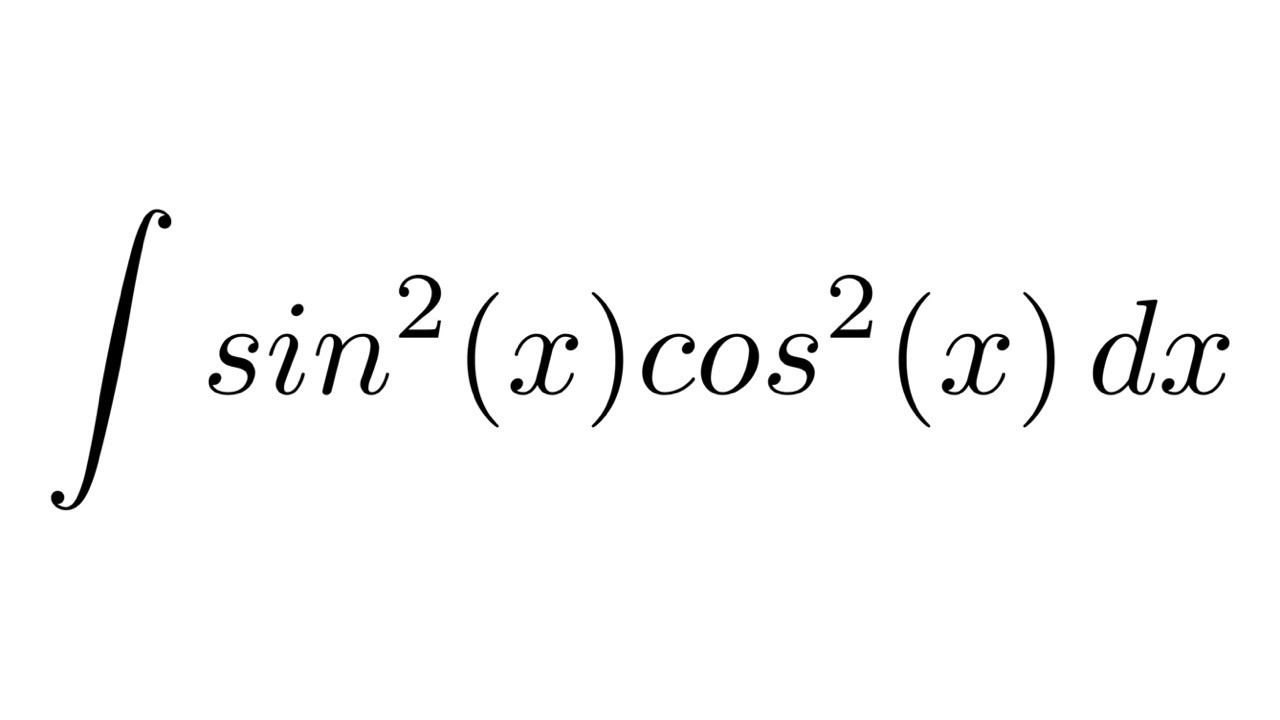De betoverende wereld van trigonometrische integralen: sin(2x)cos(3x) ontrafeld

16 Aug 2024
nl
Murphy

Wiskunde, een taal die de mysteries van het universum ontrafelt, zit vol elegante vergelijkingen en fascinerende concepten. Een van die intrigerende gebieden is de wereld van trigonometrische integralen, waar we de interactie tussen hoeken en zijden in driehoeken verkennen door de lens van calculus.

In deze wiskundige verkenningstocht richten we onze aandacht op een specifieke integraal: de integraal van sin(2x)cos(3x). Deze integraal, die op het eerste gezicht misschien complex lijkt, onthult een reeks elegante technieken en toepassingen die licht werpen op de schoonheid en kracht van calculus.

De integraal van sin(2x)cos(3x) is meer dan alleen een academische oefening; het heeft praktische toepassingen in verschillende wetenschappelijke disciplines. In de natuurkunde, bijvoorbeeld, worden integralen van trigonometrische functies gebruikt om de beweging van oscillerende systemen, zoals slingers en veren, te beschrijven. In de elektrotechniek helpen ze ons de eigenschappen van wisselstroomcircuits te analyseren.

Voordat we ons verdiepen in de details van het integreren van sin(2x)cos(3x), laten we eerst de basisprincipes van trigonometrische identiteiten en integratie herzien. Trigonometrische identiteiten zijn vergelijkingen die gelden voor alle waarden van de betrokken variabelen. Deze identiteiten zijn essentiële hulpmiddelen bij het vereenvoudigen van trigonometrische uitdrukkingen en het oplossen van trigonometrische vergelijkingen.

Een van de belangrijkste trigonometrische identiteiten die we in dit geval zullen gebruiken, is de product-tot-som-formule:

sin(a)cos(b) = (1/2)[sin(a + b) + sin(a - b)]

Met behulp van deze identiteit kunnen we de integraal van sin(2x)cos(3x) herschrijven als de som van twee eenvoudigere integralen, waardoor het integratieproces aanzienlijk wordt vereenvoudigd. De resulterende integralen kunnen vervolgens worden opgelost met behulp van standaard integratietechnieken, zoals substitutie of integratie door delen.

Voordelen van het begrijpen van trigonometrische integralen

Het begrijpen van trigonometrische integralen, zoals de integraal van sin(2x)cos(3x), heeft verschillende voordelen:

Verbetert het probleemoplossend vermogen in calculus en trigonometrie.
Biedt hulpmiddelen voor het oplossen van real-world problemen in natuurkunde, techniek en andere wetenschappen.
Verdiept het begrip van de relatie tussen trigonometrie en calculus.

Veelgestelde vragen

Vraag: Wat is de integraal van sin(2x)cos(3x)?

Antwoord: De integraal van sin(2x)cos(3x) kan worden gevonden met behulp van de product-tot-som-identiteit en standaard integratietechnieken. Het resultaat is -(1/10)cos(5x) - (1/2)cos(x) + C, waarbij C de integratieconstante is.

Vraag: Wat zijn enkele toepassingen van trigonometrische integralen in de natuurkunde?

Antwoord: Trigonometrische integralen worden in de natuurkunde gebruikt om de beweging van oscillerende systemen, zoals slingers en veren, te beschrijven. Ze worden ook gebruikt bij de studie van golven, zoals geluidsgolven en lichtgolven.

Conclusie

De integraal van sin(2x)cos(3x) is een fascinerend voorbeeld van hoe trigonometrische identiteiten en integratietechnieken kunnen worden gecombineerd om wiskundige problemen op te lossen. Door de kracht van deze concepten te begrijpen, kunnen we de complexiteit van trigonometrische integralen ontrafelen en hun toepassingen in verschillende wetenschappelijke disciplines waarderen.

De reis door de wereld van trigonometrische integralen gaat verder dan het oplossen van vergelijkingen; het gaat om het waarderen van de elegantie en schoonheid van wiskunde en het herkennen van de diepgaande impact ervan op ons begrip van de wereld om ons heen.