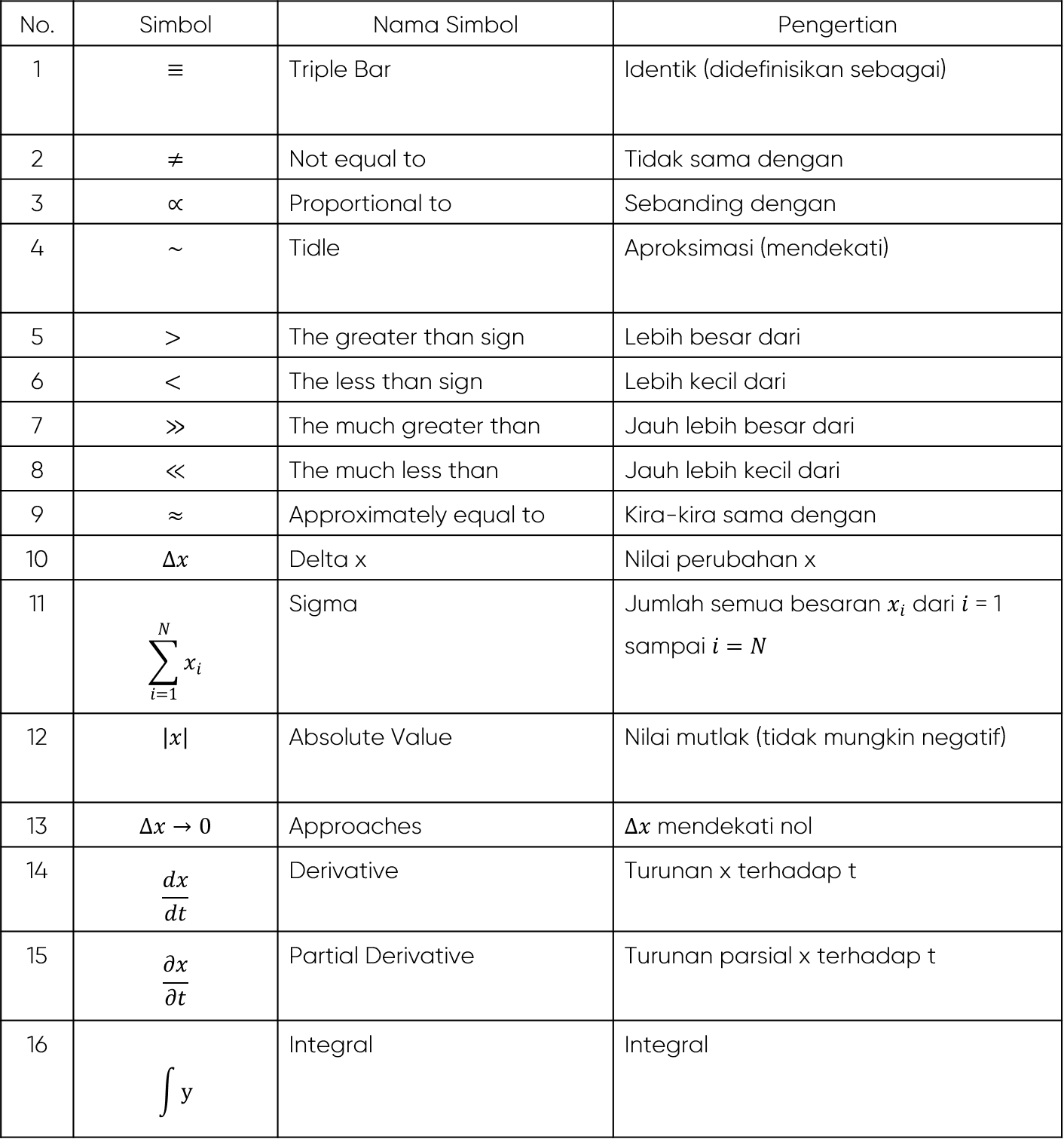
Pernahkah anda terserempak dengan simbol tanda seru (!) selepas nombor dalam persamaan matematik dan tertanya-tanya apa maksudnya? Jangan risau, anda tidak keseorangan! Simbol ini, yang dikenali sebagai faktorial dalam matematik, memainkan peranan penting dalam pelbagai pengiraan. Mari kita terokai dunia faktorial, memahami kepentingannya, dan meneroka pelbagai aplikasi yang menarik.
Bayangkan anda mempunyai 3 buku berwarna berbeza - merah, biru dan hijau - dan anda ingin menyusunnya di rak buku. Berapa banyak cara yang berbeza yang boleh anda susun?
Nah, anda mempunyai 3 pilihan untuk buku pertama. Setelah anda meletakkan buku pertama, anda mempunyai 2 pilihan untuk buku kedua, dan akhirnya hanya 1 pilihan untuk buku terakhir. Jadi, jumlah susunan yang mungkin ialah 3 x 2 x 1 = 6. Inilah di mana faktorial datang - ia mewakili pendaraban semua integer positif dari 1 hingga nombor yang diberikan. Dalam kes ini, 3! (dibaca sebagai "tiga faktorial") sama dengan 6.
Faktorial, yang diwakili oleh simbol tanda seru, mungkin kelihatan seperti konsep yang mudah, tetapi ia membentuk asas untuk pelbagai konsep matematik kompleks dalam bidang seperti kebarangkalian, statistik, dan kalkulus. Memahami faktorial adalah penting untuk menyelesaikan banyak masalah dunia sebenar, terutamanya dalam bidang yang melibatkan susunan atau kombinasi.
Sejarah faktorial boleh dikesan kembali ke zaman purba, dengan ahli matematik India meneroka konsep ini seawal abad ke-12. Walau bagaimanapun, notasi tanda seru (!) untuk faktorial diperkenalkan kemudian, pada abad ke-19, oleh ahli matematik Perancis, Christian Kramp.
Salah satu masalah utama yang berkaitan dengan faktorial ialah mereka boleh menjadi sangat besar dengan cepat apabila nombor itu bertambah. Sebagai contoh, 10! sama dengan 3,628,800. Ini boleh menjadikan pengiraan manual mencabar, tetapi untungnya, kalkulator dan komputer boleh mengira faktorial besar dengan mudah.
Kelebihan dan Kekurangan Simbol Tanda Seru dalam Matematik
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pengiraan susunan dan kombinasi. | Boleh menjadi sangat besar dengan cepat, menjadikan pengiraan manual sukar. |
| Notasi ringkas dan mudah difahami. | Penggunaannya terhad kepada integer positif. |
Amalan Terbaik untuk Melaksanakan Simbol Tanda Seru dalam Matematik
Berikut adalah beberapa amalan terbaik untuk menggunakan faktorial:
- Fahami konsep faktorial: Pastikan anda memahami konsep faktorial sebelum menggunakannya dalam pengiraan.
- Gunakan kalkulator atau komputer untuk nombor besar: Untuk nombor besar, gunakan kalkulator atau komputer untuk mengelakkan kesilapan dan menjimatkan masa.
- Permudahkan ungkapan faktorial: Permudahkan ungkapan faktorial sebelum melakukan pengiraan untuk menjadikannya lebih mudah.
- Periksa jawapan anda: Sentiasa semak jawapan anda, terutamanya apabila mengendalikan nombor besar.
- Rujuk sumber tambahan: Jika anda menghadapi masalah dengan faktorial, rujuk buku teks, laman web, atau aplikasi matematik untuk mendapatkan maklumat lanjut.
Contoh Nyata Faktorial
Berikut adalah beberapa contoh nyata tentang bagaimana faktorial digunakan:
- Kebarangkalian: Mengira kebarangkalian untuk memenangi loteri melibatkan faktorial, kerana ia menentukan bilangan cara yang mungkin untuk memilih nombor yang menang.
- Statistik: Faktorial digunakan dalam statistik untuk mengira bilangan cara yang mungkin untuk memilih sampel dari populasi.
- Sains Komputer: Dalam sains komputer, faktorial digunakan dalam algoritma untuk menyusun data dan mengira kerumitan masa.
- Fizik: Faktorial muncul dalam fizik statistik untuk mengira bilangan keadaan mikro yang mungkin dalam sistem.
- Kewangan: Faktorial digunakan dalam kewangan untuk mengira bilangan cara yang mungkin untuk melabur dalam portfolio.
Soalan Lazim tentang Simbol Tanda Seru dalam Matematik
Berikut adalah beberapa soalan lazim tentang faktorial:
- Apakah maksud simbol tanda seru (!) dalam matematik? Simbol tanda seru (!) dalam matematik mewakili faktorial bagi nombor.
- Bagaimanakah faktorial dikira? Faktorial bagi nombor dikira dengan mendarabkan semua integer positif dari 1 hingga nombor tersebut.
- Apakah 0! sama dengan? 0! sama dengan 1, mengikut konvensyen.
- Bolehkah faktorial menjadi nombor negatif? Tidak, faktorial hanya ditakrifkan untuk integer positif.
- Apakah beberapa aplikasi faktorial dalam kehidupan sebenar? Faktorial digunakan dalam pelbagai bidang seperti kebarangkalian, statistik, sains komputer, fizik, dan kewangan.
Tips dan Trik Berkaitan dengan Simbol Tanda Seru dalam Matematik
Berikut adalah beberapa tips untuk bekerja dengan faktorial:
- Ingat bahawa faktorial nombor adalah sama dengan nombor yang didarab dengan faktorial nombor sebelumnya. Contohnya, 5! = 5 x 4!.
- Gunakan kalkulator saintifik atau kalkulator dalam talian untuk mengira faktorial nombor besar.
- Cari corak dan hubungan antara faktorial untuk mempermudahkan pengiraan.
Kesimpulannya, simbol tanda seru, yang mewakili faktorial dalam matematik, adalah konsep yang kuat dengan aplikasi yang luas. Walaupun ia mungkin kelihatan menakutkan pada mulanya, memahami definisi, sejarah, dan aplikasinya boleh membuka dunia kemungkinan matematik baharu. Sama ada anda seorang pelajar, profesional, atau hanya seseorang yang ingin tahu tentang matematik, menguasai faktorial boleh meningkatkan kemahiran menyelesaikan masalah anda dan memperdalam penghargaan anda terhadap keajaiban nombor.
Tanda peringatan Tanda seru Simbol Gelombang segitiga, simbol, bermacam - The Brass Coq
Simbol Matematika Dalam Bahasa Inggris Beserta Cara Membacanya - The Brass Coq
Simbol Simbol Matematika Lengkap - The Brass Coq
Arti Simbol Bahan Kimia Berbahaya - The Brass Coq
Tanda seru, tanda seru Simbol Ikon Komputer Lingkaran Peringatan, tanda - The Brass Coq
Arti Decrease dan Cara Menghitungnya - The Brass Coq
Arti Tanda Dalam Matematika - The Brass Coq
simbol tanda seru dalam matematika - The Brass Coq
Ícone de erro sinaliza ícone Ponto de exclamação dentro de um ícone de - The Brass Coq
simbol tanda seru dalam matematika - The Brass Coq
Lambang Lambang Dalam Fisika - The Brass Coq