Rahsia Mudah Kira Keliling Segitiga Sama Sisi

09 Apr 2024
my
Murphy

Cara Mencari Keliling Segitiga Sama Sisi, Lengkap Penjelasan, Rumus dan

Pernahkah anda melihat piramid Mesir yang megah atau logo jenama terkenal yang ringkas? Apa persamaan mereka? Ya, kedua-duanya menggunakan bentuk segitiga, khususnya segitiga sama sisi! Bentuk geometri mudah ini memainkan peranan penting dalam pelbagai bidang, dari seni bina hingga reka bentuk grafik.

Memahami cara mengira keliling segitiga sama sisi adalah penting dalam pelbagai aplikasi praktikal. Sama ada anda seorang pelajar yang ingin menyelesaikan masalah matematik, seorang arkitek yang mereka bentuk struktur, atau hanya ingin menambah baik pengetahuan geometri anda, artikel ini akan membimbing anda dengan cara yang mudah dan komprehensif.

Sejak zaman dahulu lagi, konsep geometri telah menarik minat manusia. Orang Mesir kuno, misalnya, terkenal dengan pengetahuan geometri mereka yang canggih, yang mereka gunakan untuk membina struktur ikonik seperti piramid. Konsep keliling, iaitu jumlah panjang semua sisi bentuk, telah digunakan secara meluas dalam pelbagai aplikasi praktikal, seperti mengira bahan yang diperlukan untuk pembinaan pagar atau menentukan panjang sempadan sebidang tanah.

Masalah utama yang dihadapi oleh sesetengah orang ketika mengira keliling segitiga sama sisi ialah mereka lupa bahawa kesemua sisinya sama panjang. Ini boleh menyebabkan kekeliruan dan pengiraan yang salah. Namun, dengan pemahaman yang jelas tentang sifat segitiga sama sisi, prosesnya menjadi mudah.

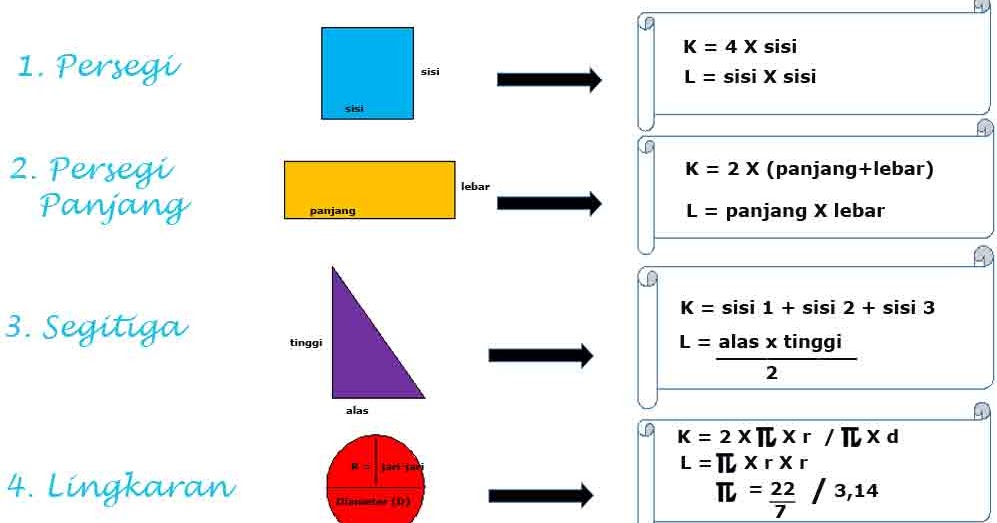
Untuk mengira keliling segitiga sama sisi, kita hanya perlu menambah panjang ketiga-tiga sisinya. Memandangkan kesemua sisinya sama panjang, formula untuk mengira keliling adalah: Keliling = 3 x Panjang sisi. Misalnya, jika panjang satu sisi segitiga sama sisi ialah 5 cm, maka kelilingnya ialah 3 x 5 cm = 15 cm.

Kelebihan dan Kekurangan Memahami Pengiraan Keliling Segitiga Sama Sisi

Kelebihan	Kekurangan
Memudahkan penyelesaian masalah matematik dan geometri.	Mungkin tidak begitu berguna untuk bentuk geometri lain yang lebih kompleks.
Dapat diaplikasikan dalam pelbagai bidang seperti seni bina, reka bentuk, dan kejuruteraan.	Memerlukan pemahaman asas tentang konsep geometri.
Membantu dalam membuat anggaran yang tepat untuk projek yang melibatkan bentuk segitiga.

Lima Amalan Terbaik untuk Memahami Pengiraan Keliling Segitiga Sama Sisi

1. Fahami konsep asas: Pastikan anda memahami definisi segitiga sama sisi dan sifat-sifatnya sebelum cuba mengira kelilingnya.

2. Hafal formula: Formula untuk mengira keliling segitiga sama sisi sangat mudah: Keliling = 3 x Panjang sisi. Hafal formula ini untuk memudahkan pengiraan.

3. Latih tubi dengan contoh: Selesaikan pelbagai masalah latihan yang melibatkan pengiraan keliling segitiga sama sisi untuk mengukuhkan pemahaman anda.

4. Gunakan alat bantu visual: Lukis atau gunakan alat bantu visual seperti pembaris dan jangka lukis untuk membantu anda menggambarkan konsep dan menyelesaikan masalah dengan lebih berkesan.

5. Terus berlatih: Seperti kemahiran lain, latihan berterusan adalah kunci untuk menguasai pengiraan keliling segitiga sama sisi dan menjadikannya sesuatu yang mudah bagi anda.

Soalan Lazim

1. Apakah definisi segitiga sama sisi?
Segitiga sama sisi ialah segitiga yang ketiga-tiga sisinya sama panjang dan ketiga-tiga sudutnya sama besar (60 darjah).

2. Apakah formula untuk mengira keliling segitiga sama sisi?
Keliling = 3 x Panjang sisi

3. Bagaimanakah saya boleh mencari panjang sisi segitiga sama sisi jika saya tahu kelilingnya?
Panjang sisi = Keliling / 3

4. Apakah aplikasi praktikal untuk mengira keliling segitiga sama sisi?
Pengiraan ini berguna dalam pelbagai bidang seperti seni bina, reka bentuk, dan kejuruteraan untuk mengira bahan yang diperlukan atau menentukan dimensi struktur.

5. Apakah beberapa petua untuk mengingati formula keliling segitiga sama sisi?
Kaitkan formula dengan bentuk segitiga dan fakta bahawa semua sisinya sama. Anda juga boleh mencipta singkatan atau rima untuk membantu anda mengingati formula.

6. Apakah perbezaan antara keliling dan luas?
Keliling ialah jumlah panjang semua sisi bentuk, manakala luas ialah jumlah ruang yang ditutupi oleh bentuk.

7. Di manakah saya boleh mencari sumber tambahan untuk mempelajari tentang segitiga sama sisi?
Terdapat banyak buku teks matematik, laman web, dan video dalam talian yang menyediakan maklumat terperinci tentang segitiga sama sisi dan konsep geometri lain.

8. Apakah kepentingan mempelajari tentang bentuk geometri dalam kehidupan seharian?
Memahami bentuk geometri membantu kita menghargai dunia di sekeliling kita dengan lebih baik dan membolehkan kita menyelesaikan masalah praktikal dalam pelbagai bidang.

Tips dan Trik

Apabila berhadapan dengan masalah yang melibatkan keliling segitiga sama sisi, sentiasa ingat bahawa kunci penyelesaian terletak pada mengingati bahawa semua sisinya sama panjang. Gunakan maklumat ini untuk mencari panjang sisi yang tidak diketahui atau untuk mengesahkan jawapan anda.

Kesimpulannya, memahami cara mengira keliling segitiga sama sisi adalah kemahiran asas yang boleh diaplikasikan dalam pelbagai situasi praktikal. Dengan memahami konsep, menghafal formula, dan berlatih secara konsisten, anda boleh menguasai kemahiran ini dengan mudah. Mulakan dengan mengaplikasikan pengetahuan yang telah anda pelajari hari ini dan terus terokai dunia geometri yang menarik!