Pernahkah anda terfikir bagaimana jurutera merancang bangunan pencakar langit yang gah, atau bagaimana arkitek menentukan jumlah konkrit yang diperlukan untuk membina sebuah jambatan yang kukuh? Rahsianya terletak pada pemahaman yang mendalam tentang ruang tiga dimensi, dan alat utama untuk menguasai konsep ini adalah "kumpulan rumus volume bangun ruang."
Kumpulan rumus ini merupakan himpunan persamaan matematik yang membolehkan kita mengira jumlah ruang yang boleh diisi oleh sesuatu objek tiga dimensi. Daripada kubus dan kuboid yang ringkas hinggalah kepada kon, silinder, dan sfera yang lebih kompleks, setiap bangun ruang mempunyai formula uniknya sendiri. Menguasai kumpulan rumus ini membuka pintu kepada pelbagai aplikasi praktikal dalam kehidupan seharian kita.
Sejarah penggunaan rumus volume bangun ruang bermula sejak zaman Mesir purba dan Mesopotamia. Mereka menggunakan rumus-rumus ini untuk tujuan seperti pembinaan piramid, pengiraan isipadu air untuk pengairan, dan reka bentuk tembikar yang rumit. Sejak itu, ilmu geometri dan pemahaman kita tentang bentuk tiga dimensi telah berkembang dengan pesat, membawa kepada penemuan formula yang lebih kompleks dan tepat.
Kepentingan kumpulan rumus volume bangun ruang tidak boleh disangkal lagi. Dalam bidang kejuruteraan, formula ini penting untuk mereka bentuk struktur bangunan, kenderaan, dan pelbagai mesin. Dalam bidang sains, ia digunakan untuk mengira isipadu cecair, gas, dan pepejal dalam eksperimen dan penyelidikan. Malah dalam kehidupan seharian, kita menggunakan rumus ini secara tidak langsung, contohnya ketika memasak dengan menggunakan sukatan cawan dan sudu.
Walaupun kumpulan rumus volume bangun ruang menawarkan pelbagai manfaat, terdapat juga cabaran dalam mempelajarinya. Salah satu cabaran utama adalah mengingati pelbagai formula yang berbeza untuk setiap bangun ruang. Di sinilah pentingnya memahami konsep asas geometri dan turunan setiap formula, bukan sekadar menghafalnya. Selain itu, ketepatan dalam mengukur dimensi sesuatu objek adalah kritikal untuk mendapatkan pengiraan volume yang tepat.
Sebagai contoh, mari kita lihat formula untuk mengira volume kubus. Kubus ialah bangun ruang tiga dimensi dengan enam sisi yang sama saiz dan bentuknya. Formula untuk mengira volume kubus ialah sisi × sisi × sisi atau sisi³. Katakan kita mempunyai kubus dengan panjang sisi 5 cm. Untuk mengira volumenya, kita hanya perlu menggantikan nilai sisi ke dalam formula: 5 cm × 5 cm × 5 cm = 125 cm³. Jadi, volume kubus tersebut ialah 125 cm³.
Memahami konsep asas geometri dan turunan formula volume bagi setiap bangun ruang adalah kunci untuk menguasai kumpulan rumus ini. Dengan latihan dan dedikasi yang konsisten, anda boleh menguasai kemahiran mengira volume bangun ruang dan memanfaatkannya dalam pelbagai aspek kehidupan anda.
Kelebihan dan Kekurangan Kumpulan Rumus Volume Bangun Ruang
| Kelebihan | Kekurangan |
|---|---|
| Membantu menyelesaikan masalah praktikal dalam pelbagai bidang. | Memerlukan pemahaman yang baik tentang konsep geometri. |
| Meningkatkan keupayaan menyelesaikan masalah matematik. | Boleh menjadi rumit untuk mengingati pelbagai formula yang berbeza. |
| Memudahkan pengiraan isipadu objek tiga dimensi. | Ketepatan pengukuran dimensi objek sangat penting untuk mendapatkan hasil yang tepat. |
Lima Amalan Terbaik untuk Menguasai Kumpulan Rumus Volume Bangun Ruang
- Fahami konsep asas geometri: Luangkan masa untuk memahami konsep asas seperti titik, garis, satah, dan bentuk dua dimensi sebelum mendalami bentuk tiga dimensi dan volumenya.
- Pelajari turunan formula: Daripada hanya menghafal formula, cuba fahami bagaimana setiap formula dihasilkan. Ini akan memudahkan anda mengingati dan menggunakan formula dengan lebih berkesan.
- Latih tubi secara konsisten: Selesaikan pelbagai soalan latihan yang melibatkan pengiraan volume bangun ruang yang berbeza. Ini akan membantu anda mengukuhkan pemahaman anda dan meningkatkan kecekapan anda.
- Gunakan sumber pembelajaran yang pelbagai: Manfaatkan buku teks, laman web, video tutorial, dan aplikasi mudah alih untuk mempelajari kumpulan rumus volume bangun ruang dengan cara yang menarik dan berkesan.
- Jangan takut untuk bertanya: Jika anda menghadapi kesukaran memahami sesuatu konsep atau formula, jangan takut untuk bertanya kepada guru, rakan sekelas, atau pakar dalam bidang tersebut.
Lima Contoh Nyata Penggunaan Kumpulan Rumus Volume Bangun Ruang
- Jurutera Awam: Mengira jumlah konkrit yang diperlukan untuk membina asas bangunan berdasarkan pelan reka bentuk.
- Arkitek: Menentukan jumlah ruang udara di dalam sebuah bilik untuk mereka bentuk sistem penghawa dingin yang cekap.
- Saintis: Mengira isipadu cecair yang diperlukan untuk eksperimen kimia di makmal.
- Tukang Masak: Menggunakan sukatan cawan dan sudu untuk mengukur isipadu bahan masakan mengikut resipi.
- Peniaga: Menentukan saiz kotak yang sesuai untuk membungkus dan menghantar produk kepada pelanggan.
Lima Cabaran dan Penyelesaian Berkaitan Kumpulan Rumus Volume Bangun Ruang
| Cabaran | Penyelesaian |
|---|---|
| Mengingati pelbagai formula yang berbeza. | Gunakan kad imbasan atau carta untuk membantu mengingat formula. |
| Memahami konsep geometri yang kompleks. | Cari sumber pembelajaran tambahan seperti video tutorial atau buku teks yang menerangkan konsep dengan lebih terperinci. |
| Melakukan pengiraan yang tepat. | Gunakan kalkulator saintifik dan semak semula jawapan anda dengan teliti. |
| Menyelesaikan masalah praktikal yang melibatkan volume bangun ruang. | Latih tubi menyelesaikan pelbagai soalan latihan yang berkaitan dengan situasi dunia sebenar. |
| Memilih formula yang betul untuk setiap masalah. | Kenal pasti jenis bangun ruang yang terlibat dan gunakan formula yang sepadan. |
Soalan Lazim tentang Kumpulan Rumus Volume Bangun Ruang
- Apakah perbezaan antara luas permukaan dan volume? Luas permukaan merujuk kepada jumlah luas permukaan luar sesuatu objek, manakala volume merujuk kepada jumlah ruang yang boleh diisi oleh objek tersebut.
- Apakah unit ukuran yang biasa digunakan untuk volume? Unit ukuran yang biasa digunakan untuk volume termasuklah meter padu (m³), sentimeter padu (cm³), dan liter (L).
- Bagaimana jika saya terlupa formula untuk sesuatu bangun ruang? Anda boleh merujuk kepada buku teks, laman web, atau aplikasi mudah alih yang menyediakan senarai formula volume bangun ruang.
- Adakah terdapat cara yang lebih mudah untuk mempelajari kumpulan rumus ini? Ya, terdapat pelbagai teknik pembelajaran yang boleh membantu anda mengingati formula dengan lebih mudah, seperti menggunakan kad imbasan, mnemonik, atau peta minda.
- Mengapa penting untuk mempelajari kumpulan rumus volume bangun ruang? Menguasai kumpulan rumus ini penting untuk pelbagai aplikasi praktikal dalam kehidupan seharian, terutamanya dalam bidang STEM (sains, teknologi, kejuruteraan, dan matematik).
- Bagaimanakah saya boleh menggunakan pengetahuan ini dalam kerjaya masa hadapan saya? Pengetahuan tentang volume bangun ruang penting dalam pelbagai bidang kerjaya seperti kejuruteraan, seni bina, reka bentuk, dan sains.
- Adakah terdapat sumber dalam talian yang boleh membantu saya mempelajari kumpulan rumus ini? Ya, terdapat pelbagai laman web dan aplikasi mudah alih yang menyediakan tutorial interaktif, soalan latihan, dan sumber pembelajaran lain yang berkaitan dengan volume bangun ruang.
- Apakah beberapa aplikasi praktikal lain untuk kumpulan rumus volume bangun ruang? Selain daripada yang telah disebutkan, kumpulan rumus ini juga digunakan dalam bidang perubatan (mengira dos ubat), pertanian (mengira isipadu cecair baja), dan pembuatan (merekabentuk acuan untuk produk).
Tips dan Trik Mempelajari Kumpulan Rumus Volume Bangun Ruang
- Gunakan warna-warna yang berbeza untuk menandakan setiap bahagian formula dan memadankannya dengan bahagian yang sepadan pada rajah bangun ruang.
- Cipta kad imbasan dengan gambar bangun ruang pada satu sisi dan formula volumenya pada sisi yang lain.
- Cari video tutorial di YouTube yang menerangkan konsep volume bangun ruang dengan cara yang mudah difahami.
- Bina model bangun ruang tiga dimensi menggunakan kertas, kadbod, atau tanah liat untuk membantu anda memvisualisasikan bentuk dan dimensinya.
- Bergabung dengan rakan sekelas untuk membentuk kumpulan belajar dan berlatih menyelesaikan masalah bersama-sama.
Sebagai kesimpulannya, kumpulan rumus volume bangun ruang memainkan peranan penting dalam kehidupan kita, daripada membantu jurutera merancang infrastruktur yang mengagumkan hinggalah membolehkan kita mengukur bahan masakan dengan tepat di dapur. Walaupun penguasaan kumpulan rumus ini memerlukan usaha dan dedikasi, manfaat yang diperoleh adalah tidak ternilai. Dengan memahami konsep asas geometri, berlatih secara konsisten, dan memanfaatkan pelbagai sumber pembelajaran, anda boleh membuka kunci rahsia mengira ruang dan menggunakan pengetahuan ini untuk mencapai kejayaan dalam pelbagai bidang.
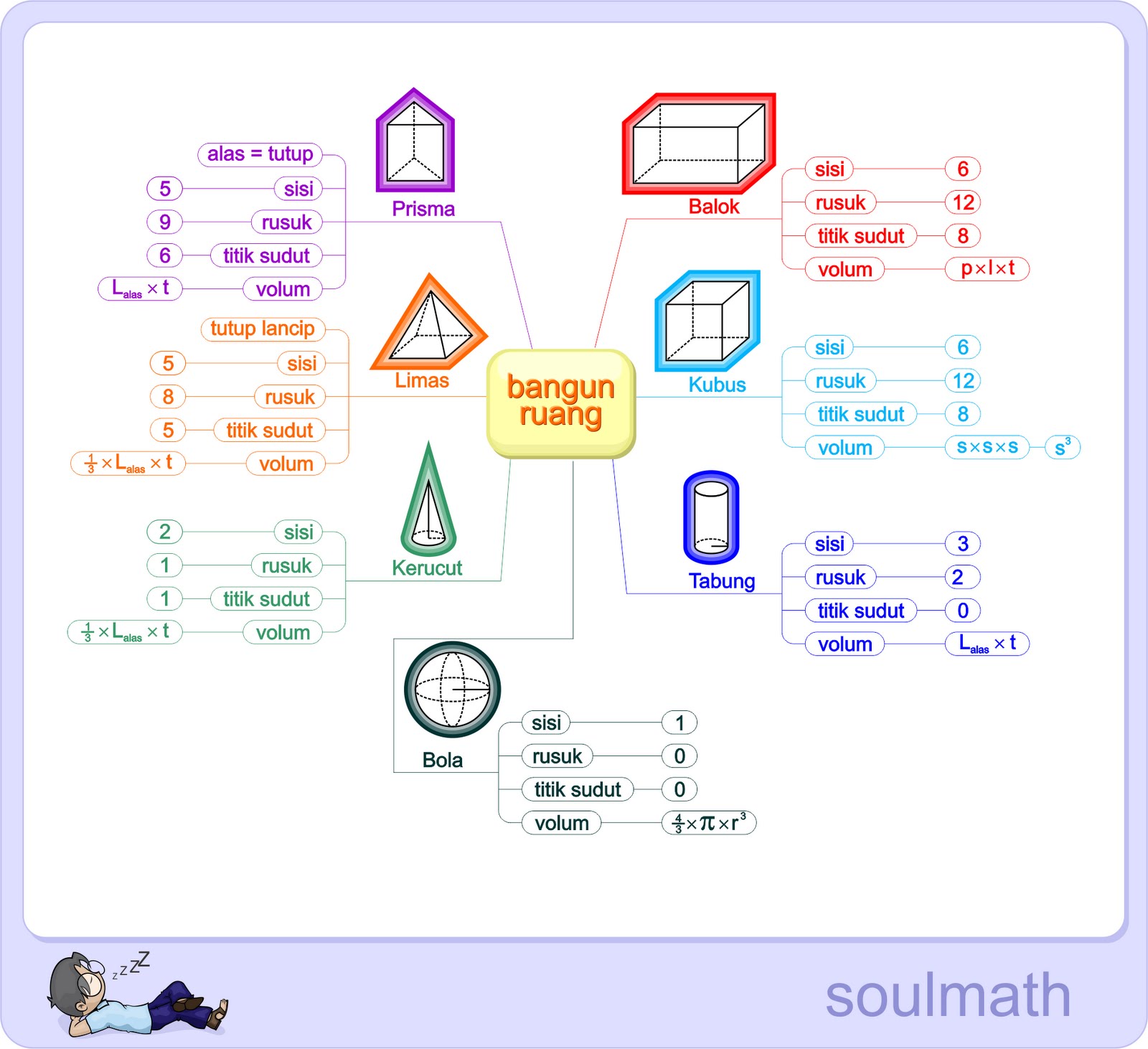
Rumus Bangun Ruang: Kubus, Balok, Tabung, Bola dll - The Brass Coq
kumpulan rumus volume bangun ruang - The Brass Coq
Volume Bangun Ruang Tabung Adalah 3 Kali Dari Volume Bangun Ruang - The Brass Coq
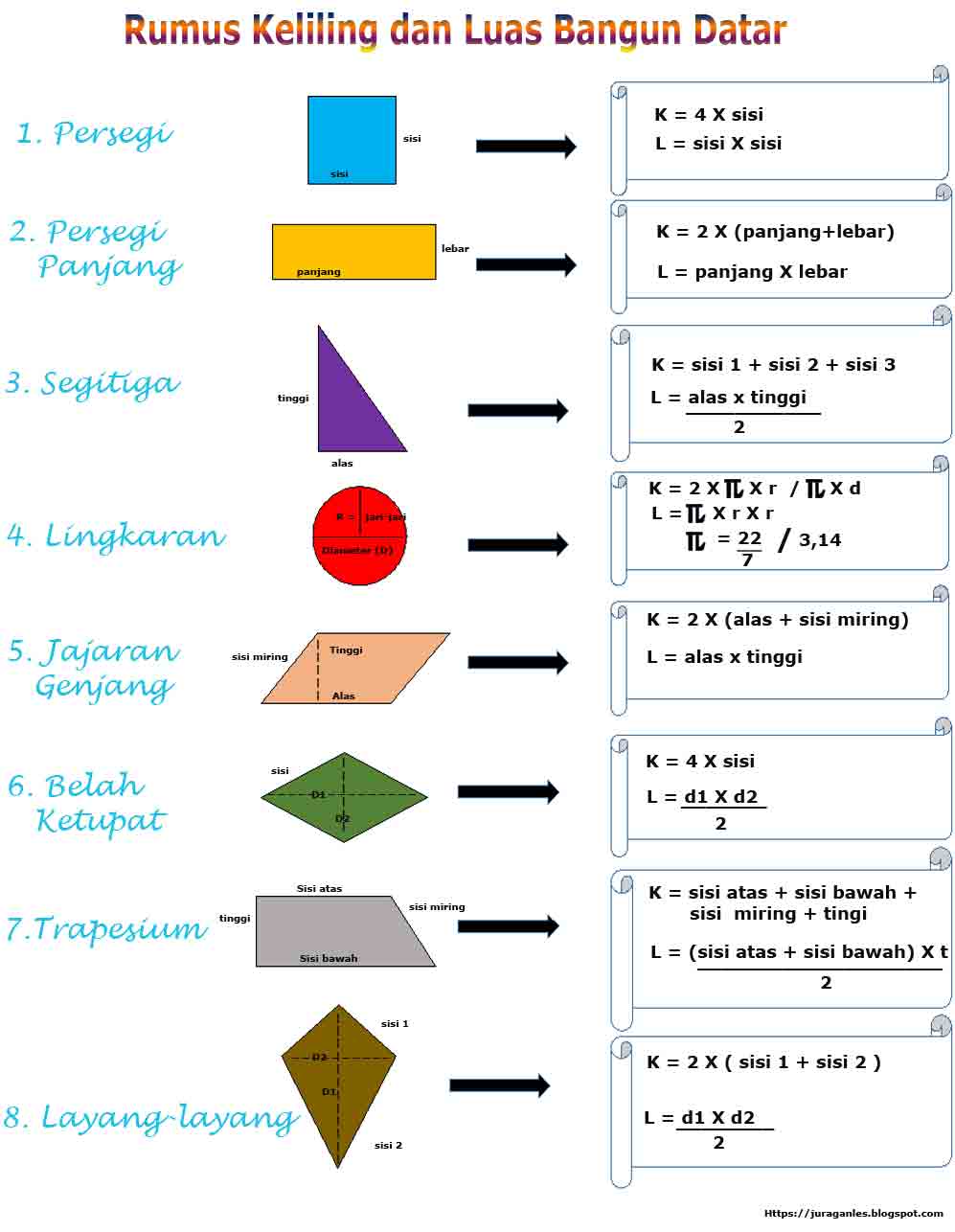
Rumus Keliling dan Luas Bangun Datar Lengkap beserta Gambar ~ Juragan Les - The Brass Coq
Rumus Rumus Matematika Smp Kelas 7 - The Brass Coq
Terbaru 28+ Rumus Bangun Ruang Kubus - The Brass Coq
kumpulan rumus volume bangun ruang - The Brass Coq
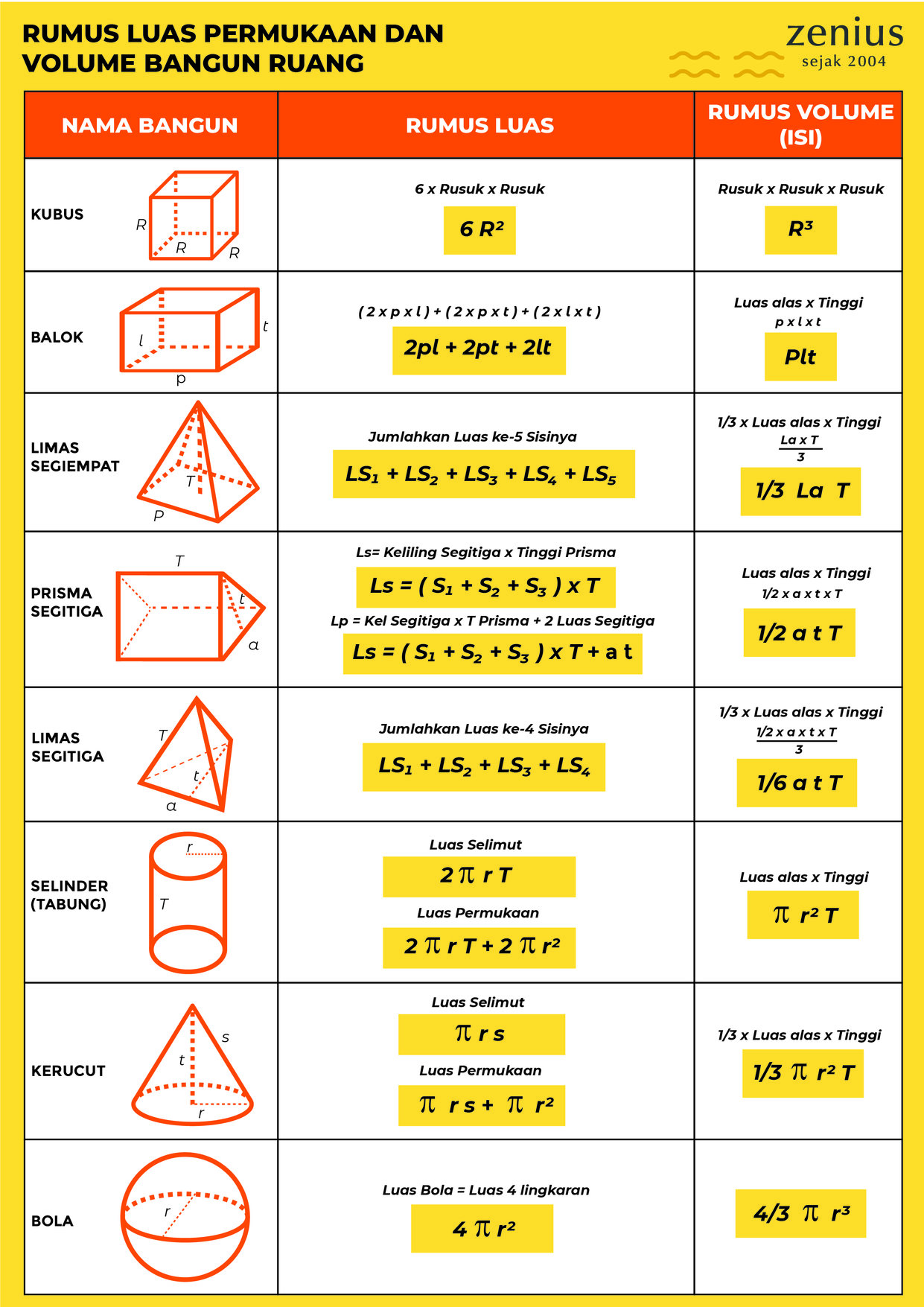
Rumus Bangun Ruang Menghitung Volume Luas Permukaan Dan Contoh Soal - The Brass Coq
Detail Rumus Bangun Ruang Dan Contoh Soal Koleksi Nomer 55 - The Brass Coq