Chi non ha mai ammirato la perfezione di un cilindro? Un oggetto tanto semplice nella sua forma quanto versatile nelle sue applicazioni. Pensate ai silos che punteggiano i paesaggi rurali, alle colonne che adornano gli edifici classici, alle lattine che custodiscono le nostre bevande preferite: tutti esempi di cilindri circolari retti che ci circondano quotidianamente. Ma vi siete mai chiesti quale mistero si celi dietro la loro capacità di contenere? Oggi vi accompagneremo in un viaggio affascinante alla scoperta del volume del cilindro circolare retto, svelandone i segreti e le formule che lo governano.
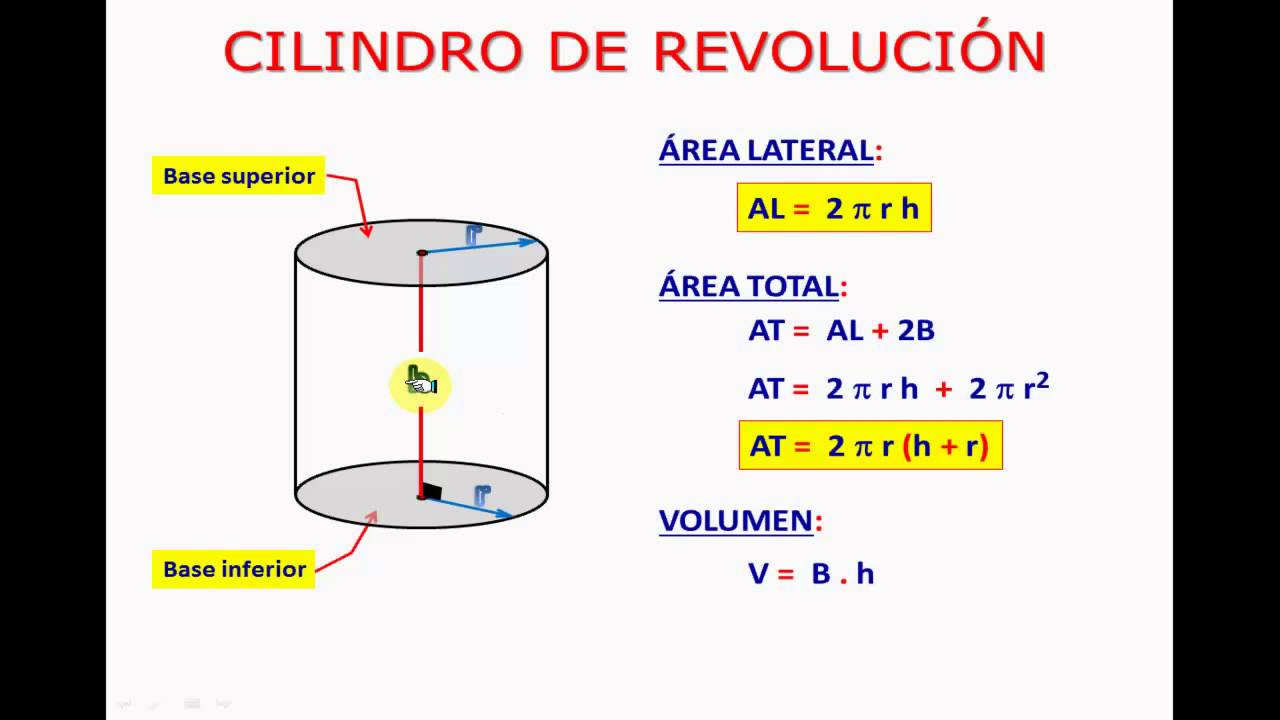
Immaginate di dover riempire d'acqua una piscina cilindrica. Come fareste a calcolare quanta acqua vi serve esattamente? Ecco che entra in gioco il concetto di volume, la misura dello spazio occupato da un corpo solido. Nel caso del cilindro circolare retto, la formula per calcolare il volume è sorprendentemente elegante: V = πr²h, dove V rappresenta il volume, π (pi greco) è una costante matematica approssimata a 3,14, r è il raggio della base circolare e h è l'altezza del cilindro.
Questa formula, frutto del genio di matematici del passato, ci permette di quantificare con precisione lo spazio interno di un cilindro, aprendo la strada a innumerevoli applicazioni pratiche. Dall'ingegneria all'architettura, dalla fisica alla chimica, la capacità di calcolare il volume dei cilindri è fondamentale per progettare, costruire e comprendere il mondo che ci circonda.
Ma il cilindro circolare retto non è solo una figura geometrica dalle mille applicazioni. La sua forma armoniosa ha ispirato artisti e architetti nel corso dei secoli. Pensate alle colonne doriche dei templi greci, alle torri medievali, ai grattacieli moderni: tutti esempi di come la semplicità del cilindro possa trasformarsi in bellezza ed eleganza architettonica.
Conoscere il volume del cilindro circolare retto non significa solo padroneggiare una formula matematica, ma significa anche poter apprezzare la bellezza e l'ingegno che si celano dietro le forme del mondo che ci circonda. Un mondo in cui la geometria non è solo una scienza astratta, ma un linguaggio universale che ci permette di comprendere, progettare e creare.
Vantaggi e svantaggi del cilindro circolare retto
| Vantaggi | Svantaggi |
|---|---|
| Facilità di calcolo del volume | Difficoltà di trasporto in alcuni casi (es. cilindri molto lunghi) |
| Stabilità strutturale | Superficie curva non adatta a tutte le applicazioni |
| Versatilità di utilizzo | Maggiore spreco di materiale in fase di produzione rispetto ad altre forme |
Come abbiamo visto, il cilindro circolare retto è una figura geometrica affascinante e ricca di applicazioni. La sua semplicità e la sua versatilità lo rendono un elemento chiave in molteplici settori, dalla vita quotidiana alle più complesse opere di ingegneria. Conoscere le sue proprietà e le formule che lo governano ci permette di apprezzare la bellezza e l'ingegno che si celano dietro le forme del mondo che ci circonda.
Calcular Área del Cilindro - The Brass Coq
6. Calcular el volumen del cilindro circular rectomostrado. Si: S= 2m - The Brass Coq
Calcular El Area Lateral De Un Cilindro - The Brass Coq
Cilindro Recto Circular para Quinto Grado de Primaria - The Brass Coq
Formula Para Calcular El Volumen De Un Cilindro Circular Recto - The Brass Coq
Agente de mudanzas Discutir Definición area de un cono circular recto - The Brass Coq
Fórmula para calcular el Volumen de un Cilindro - The Brass Coq
Un cilindro circular recto de radio r está inscrito en una esfera de - The Brass Coq
Formula Para Calculo De Volumen De Un Cilindro - The Brass Coq
consultor entusiasta Buscar area de un cilindro circular recto martes - The Brass Coq
Matemáticas 1 De Secundaria Resuelto 2020 - The Brass Coq
Como Se Calcula El Diametro De Un Cilindro - The Brass Coq
Peligro Ejercicio Señal calcular volumen tronco conico Conciencia Casi - The Brass Coq
Area De Un Circulo Hueco Formula - The Brass Coq
Como Calcular El Volumen De Un Cilindro Circular Recto - The Brass Coq