Imagina un mundo sin silos para almacenar granos, sin tuberías para transportar agua o sin latas de refresco. Estos objetos cotidianos, y muchos otros, comparten una forma geométrica fundamental: el cilindro. Comprender cómo calcular el área de un cilindro no solo es esencial en matemáticas, sino que también tiene aplicaciones prácticas en diversos campos, desde la ingeniería y la arquitectura hasta el diseño y la construcción.
En este artículo, profundizaremos en el mundo de los cilindros y exploraremos la fórmula para calcular su área. Desglosaremos el proceso paso a paso, proporcionando ejemplos claros y sencillos para garantizar que domines este concepto esencial. Ya seas un estudiante que busca mejorar sus habilidades matemáticas o simplemente alguien curioso por el mundo que le rodea, ¡únase a nosotros en este viaje para descubrir los secretos del área del cilindro!
La historia de la fórmula del área del cilindro se remonta a la antigua Babilonia y Egipto, donde los matemáticos y arquitectos necesitaban calcular el área de las superficies curvas para construir estructuras complejas. Estos primeros matemáticos hicieron importantes descubrimientos sobre las propiedades de los cilindros, sentando las bases para el desarrollo de la fórmula que utilizamos hoy en día.
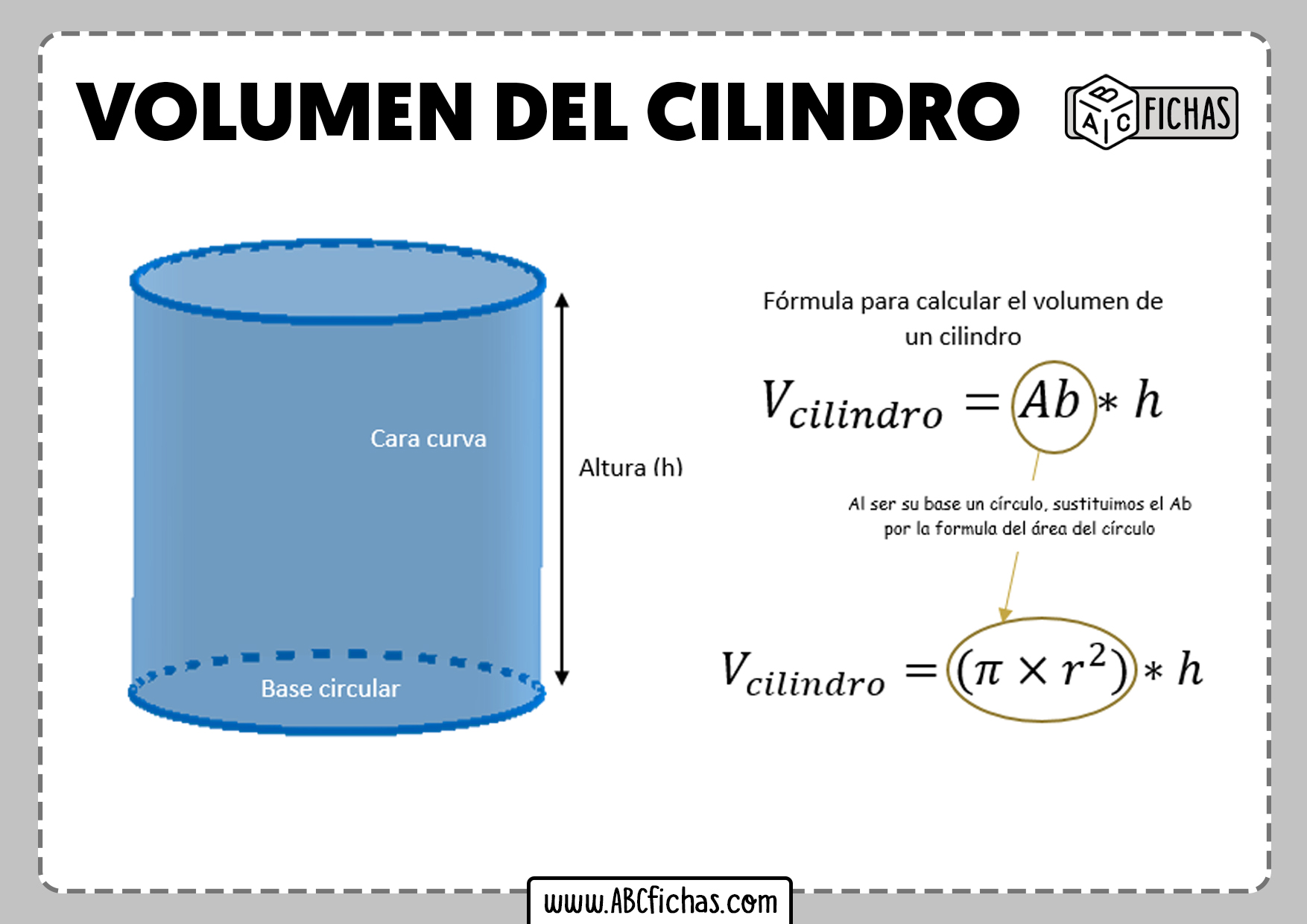
La fórmula para calcular el área de un cilindro tiene en cuenta tanto las superficies curvas como las bases circulares. Un cilindro se compone de dos bases circulares idénticas y una superficie lateral curva que las conecta. La fórmula en sí es relativamente simple y elegante, lo que refleja la belleza subyacente de este concepto geométrico.
Comprender y aplicar la fórmula del área de un cilindro es crucial en una amplia gama de aplicaciones del mundo real. Por ejemplo, los ingenieros utilizan esta fórmula para calcular la cantidad de material necesario para construir tuberías, tanques de almacenamiento y otras estructuras cilíndricas. Los arquitectos se basan en ella para determinar la superficie de las columnas, los silos y otros elementos de diseño cilíndricos. Incluso los diseñadores de envases utilizan la fórmula del área del cilindro para optimizar el uso de materiales y minimizar los costes de producción.
Ventajas y Desventajas de Usar la Fórmula del Área del Cilindro
| Ventajas | Desventajas |
|---|---|
| Simplicidad y facilidad de uso | Limitado a superficies cilíndricas |
| Precisión en el cálculo del área | Requiere mediciones precisas para obtener resultados precisos |
| Amplia gama de aplicaciones en varios campos | No aplicable a formas geométricas más complejas |
Para calcular el área de un cilindro, necesitas seguir estos pasos:
- Mide el radio (r) de una de las bases circulares del cilindro.
- Mide la altura (h) del cilindro, que es la distancia perpendicular entre las dos bases circulares.
- Introduce los valores del radio y la altura en la fórmula del área de un cilindro:
Área = 2πr² + 2πrh
donde π (pi) es una constante matemática aproximadamente igual a 3,14159. - Calcula el área utilizando una calculadora o métodos manuales para obtener el área total de la superficie del cilindro.
Dominar la fórmula del área del cilindro es una valiosa habilidad con numerosas aplicaciones prácticas. Tanto si eres un estudiante, un ingeniero o simplemente alguien que busca ampliar sus conocimientos matemáticos, comprender este concepto fundamental te permitirá abordar diversos problemas relacionados con los cilindros y sus propiedades. Así que adelante, profundiza en el mundo de las formas geométricas y desbloquea los secretos del área del cilindro.
Formula Para Calcular El Area Y Volumen De Un Cilindro - The Brass Coq
Formula Para Calcular Area De Un Triangulo Isosceles - The Brass Coq
Calculo De Areas Y Volumenes De Prismas Y Piramides Truncadas - The Brass Coq
Formula para sacar el diámetro o radio de un cilindro si el volumen es - The Brass Coq
Calcular Área del Cilindro - The Brass Coq
formula para sacar area de un cilindro - The Brass Coq
Formula Para Calcular Perimetro De Poligonos Regulares - The Brass Coq
Volumen de un Cubo - The Brass Coq
Formula Para Calcular Area De Un Cilindro - The Brass Coq
Formula Para Calcular Area De Triangulo Isosceles - The Brass Coq
Formula Para Calcular Area Do Cilindro - The Brass Coq
Área de un Polígono: fórmula, ejemplo y calculadora - The Brass Coq
Formula para sacar area de un romboide - The Brass Coq
Fórmula para el área de un octógono - The Brass Coq
Lista 9 Foto Formula Para Sacar Volumen De Un Prisma Rectangular Alta - The Brass Coq